36, Valid Sudoku

I Problem

Determine if a 9 x 9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:

1. Each row must contain the digits 1-9 without repetition.
2. Each column must contain the digits 1-9 without repetition.
3. Each of the nine 3 x 3 sub-boxes of the grid must contain the digits 1-9 without repetition.

Note:

• A Sudoku board (partially filled) could be valid but is not necessarily solvable.
• Only the filled cells need to be validated according to the mentioned rules.

Example 1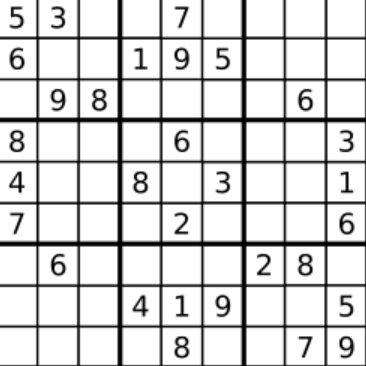

Input: board =

[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]

Output: true

Example 2
Input: board =

[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]

Output: false
Explanation: Same as Example 1, except with the 5 in the top left corner being modified to 8. Since there are two 8's in the top left 3x3 sub-box, it is invalid.

Constraints

• board.length == 9
• board[i].length == 9
• board[i][j] is a digit 1-9 or '.'.

Related Topics

• Array
• Hash Table
• Matrix

II Solution

Approach 1: Traversal Three Times

pub fn is_valid_sudoku(board: Vec<Vec<char>>) -> bool {
    let len = board.len();
    let mut counter = HashMap::with_capacity(len);
    let is_valid = |ch: char, counter: &mut HashMap<char, i32>| {
        if ch != '.' {
            counter.entry(ch).and_modify(|v| *v += 1).or_insert(1);
            return counter[&ch] < 2;
        };

        true
    };

    let mut is_row_valid = || {
        for i in 0..len {
            counter.clear();
            for &ch in board[i].iter() {
                if !is_valid(ch, &mut counter) {
                    return false;
                }
            }
        }
        true
    };
    if !is_row_valid() {
        return false;
    }

    let mut is_col_valid = || {
        for i in 0..len {
            counter.clear();
            for j in 0..len {
                if !is_valid(board[j][i], &mut counter) {
                    return false;
                }
            }
        }
        true
    };
    if !is_col_valid() {
        return false;
    }

    let mut is_sub_boxes_valid = || {
        for i in 0..len {
            for j in 0..len {
                if i % 3 == 0 && j % 3 == 0 {
                    counter.clear();
                    for r in 0..3 {
                        for c in 0..3 {
                            if !is_valid(board[i + r][j + c], &mut counter) {
                                return false;
                            }
                        }
                    }
                }
            }
        }
        true
    };
    is_sub_boxes_valid()
}

BiPredicate<Character, Map<Character, Integer>> isValid = (ch, counter) -> {
    if (ch != '.') {
        counter.put(ch, counter.getOrDefault(ch, 0) + 1);
        return counter.get(ch) < 2;
    }

    return true;
};

BiPredicate<char[][], Map<Character, Integer>> isRowValid = (board, counter) -> {
    for (int i = 0; i < board.length; i++) {
        counter.clear();
        for (int j = 0; j < board.length; j++) {
            if (!this.isValid.test(board[i][j], counter)) {
                return false;
            }
        }
    }

    return true;
};

BiPredicate<char[][], Map<Character, Integer>> isColValid = (board, counter) -> {
    for (int i = 0; i < board.length; i++) {
        counter.clear();
        for (int j = 0; j < board.length; j++) {
            if (!this.isValid.test(board[j][i], counter)) {
                return false;
            }
        }
    }

    return true;
};

BiPredicate<char[][], Map<Character, Integer>> isSubBoxesValid = (board, counter) -> {
    for (int i = 0; i < board.length; i++) {
        for (int j = 0; j < board.length; j++) {
            if (i % 3 == 0 && j % 3 == 0) {
                counter.clear();
                for (int r = 0; r < 3; r++) {
                    for (int c = 0; c < 3; c++) {
                        if (!this.isValid.test(board[i + r][j + c], counter)) {
                            return false;
                        }
                    }
                }
            }
        }
    }

    return true;
};

public boolean isValidSudoku(char[][] board) {
    int len = board.length;
    Map<Character, Integer> counter = new HashMap<>(len);

    if (!this.isRowValid.test(board, counter)) {
        return false;
    }

    if (!this.isColValid.test(board, counter)) {
        return false;
    }

    return this.isSubBoxesValid.test(board, counter);
}

Approach 2: Traversal Once

pub fn is_valid_sudoku(board: Vec<Vec<char>>) -> bool {
    let mut rows = [[0; 9]; 9];
    let mut cols = [[0; 9]; 9];
    let mut subboxes = [[[0; 3]; 3]; 9];

    for i in 0..9 {
        for j in 0..9 {
            let ch = board[i][j];
            if ch != '.' {
                let idx = (ch as u8 - b'1') as usize;
                rows[i][idx] += 1;
                cols[j][idx] += 1;
                subboxes[idx][i / 3][j / 3] += 1;

                if rows[i][idx] > 1 || cols[j][idx] > 1 || subboxes[idx][i / 3][j / 3] > 1 {
                    return false;
                }
            }
        }
    }

    true
}

public boolean isValidSudoku(char[][] board) {
    int[][] rows = new int[9][9];
    int[][] cols = new int[9][9];
    int[][][] subboxes = new int[3][3][9];

    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            char ch = board[i][j];
            if (ch != '.') {
                int idx = ch - '1';
                rows[i][idx]++;
                cols[j][idx]++;
                subboxes[i / 3][j / 3][idx]++;
                
                if (rows[i][idx] > 1 || cols[j][idx] > 1 || subboxes[i / 3][j / 3][idx] > 1) {
                    return false;
                }
            }
        }
    }

    return true;
}