36, 有效的数独

一、题目描述

请你判断一个9 x 9的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。

1. 数字1-9在每一行只能出现一次。
2. 数字1-9在每一列只能出现一次。
3. 数字1-9在每一个以粗实线分隔的3x3宫内只能出现一次。（请参考示例图）

注意：

• 一个有效的数独（部分已被填充）不一定是可解的。
• 只需要根据以上规则，验证已经填入的数字是否有效即可。
• 空白格用'.'表示。

示例 1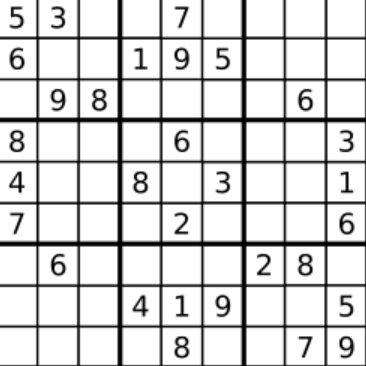

输入: board =

[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]

输出: true

示例 2
输入: board =

[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]

输出: false
解释: 除了第一行的第一个数字从5改为8以外，空格内其他数字均与示例1相同。但由于位于左上角的3x3宫内有两个8存在, 因此这个数独是无效的。

提示

• board.length == 9
• board[i].length == 9
• board[i][j]是一位数字（1-9）或者'.'

相关主题

• 数组
• 哈希表
• 矩阵

二、题解

方法 1: 遍历3次

Rust

pub fn is_valid_sudoku(board: Vec<Vec<char>>) -> bool {
    let len = board.len();
    let mut counter = HashMap::with_capacity(len);
    let is_valid = |ch: char, counter: &mut HashMap<char, i32>| {
        if ch != '.' {
            counter.entry(ch).and_modify(|v| *v += 1).or_insert(1);
            return counter[&ch] < 2;
        };

        true
    };

    let mut is_row_valid = || {
        for i in 0..len {
            counter.clear();
            for &ch in board[i].iter() {
                if !is_valid(ch, &mut counter) {
                    return false;
                }
            }
        }
        true
    };
    if !is_row_valid() {
        return false;
    }

    let mut is_col_valid = || {
        for i in 0..len {
            counter.clear();
            for j in 0..len {
                if !is_valid(board[j][i], &mut counter) {
                    return false;
                }
            }
        }
        true
    };
    if !is_col_valid() {
        return false;
    }

    let mut is_sub_boxes_valid = || {
        for i in 0..len {
            for j in 0..len {
                if i % 3 == 0 && j % 3 == 0 {
                    counter.clear();
                    for r in 0..3 {
                        for c in 0..3 {
                            if !is_valid(board[i + r][j + c], &mut counter) {
                                return false;
                            }
                        }
                    }
                }
            }
        }
        true
    };
    is_sub_boxes_valid()
}

Java

BiPredicate<Character, Map<Character, Integer>> isValid = (ch, counter) -> {
    if (ch != '.') {
        counter.put(ch, counter.getOrDefault(ch, 0) + 1);
        return counter.get(ch) < 2;
    }

    return true;
};

BiPredicate<char[][], Map<Character, Integer>> isRowValid = (board, counter) -> {
    for (int i = 0; i < board.length; i++) {
        counter.clear();
        for (int j = 0; j < board.length; j++) {
            if (!this.isValid.test(board[i][j], counter)) {
                return false;
            }
        }
    }

    return true;
};

BiPredicate<char[][], Map<Character, Integer>> isColValid = (board, counter) -> {
    for (int i = 0; i < board.length; i++) {
        counter.clear();
        for (int j = 0; j < board.length; j++) {
            if (!this.isValid.test(board[j][i], counter)) {
                return false;
            }
        }
    }

    return true;
};

BiPredicate<char[][], Map<Character, Integer>> isSubBoxesValid = (board, counter) -> {
    for (int i = 0; i < board.length; i++) {
        for (int j = 0; j < board.length; j++) {
            if (i % 3 == 0 && j % 3 == 0) {
                counter.clear();
                for (int r = 0; r < 3; r++) {
                    for (int c = 0; c < 3; c++) {
                        if (!this.isValid.test(board[i + r][j + c], counter)) {
                            return false;
                        }
                    }
                }
            }
        }
    }

    return true;
};

public boolean isValidSudoku(char[][] board) {
    int len = board.length;
    Map<Character, Integer> counter = new HashMap<>(len);

    if (!this.isRowValid.test(board, counter)) {
        return false;
    }

    if (!this.isColValid.test(board, counter)) {
        return false;
    }

    return this.isSubBoxesValid.test(board, counter);
}

方法 2: 遍历1次

Rust

pub fn is_valid_sudoku(board: Vec<Vec<char>>) -> bool {
    let mut rows = [[0; 9]; 9];
    let mut cols = [[0; 9]; 9];
    let mut subboxes = [[[0; 3]; 3]; 9];

    for i in 0..9 {
        for j in 0..9 {
            let ch = board[i][j];
            if ch != '.' {
                let idx = (ch as u8 - b'1') as usize;
                rows[i][idx] += 1;
                cols[j][idx] += 1;
                subboxes[idx][i / 3][j / 3] += 1;

                if rows[i][idx] > 1 || cols[j][idx] > 1 || subboxes[idx][i / 3][j / 3] > 1 {
                    return false;
                }
            }
        }
    }

    true
}

Java

public boolean isValidSudoku(char[][] board) {
    int[][] rows = new int[9][9];
    int[][] cols = new int[9][9];
    int[][][] subboxes = new int[3][3][9];

    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            char ch = board[i][j];
            if (ch != '.') {
                int idx = ch - '1';
                rows[i][idx]++;
                cols[j][idx]++;
                subboxes[i / 3][j / 3][idx]++;
                
                if (rows[i][idx] > 1 || cols[j][idx] > 1 || subboxes[i / 3][j / 3][idx] > 1) {
                    return false;
                }
            }
        }
    }

    return true;
}