968, 监控二叉树

一、题目描述

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1

输入: root = [0, 0, null, 0, 0]
输出: 1
解释: 如图所示，一台摄像头足以监控所有节点。

示例 2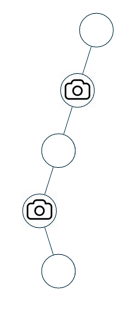

输入: root = [0, 0, null, 0, null, 0, null, null, 0]
输出: 2
解释: 需要至少两个摄像头来监视树的所有节点。上图显示了摄像头放置的有效位置之一。

提示

• 给定树的节点数的范围是[1, 1000]。
• 每个节点的值都是0。

相关主题

• 树
• 深度优先搜索
• 动态规划
• 二叉树

二、题解

#[derive(Debug, PartialEq, Eq)]
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Rc<RefCell<TreeNode>>>,
    pub right: Option<Rc<RefCell<TreeNode>>>,
}

impl TreeNode {
    #[inline]
    pub fn new(val: i32) -> Self {
        TreeNode {
            val,
            left: None,
            right: None,
        }
    }
}

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

方法 1: 动态规划

pub fn min_camera_cover(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    const DFS: fn(Option<Rc<RefCell<TreeNode>>>) -> (i32, i32, i32) = 
        |root| match root {
            None => (i32::MAX / 2, 0, 0),
            Some(curr) => {
                let (la, lb, lc) = DFS(curr.borrow_mut().left.take());
                let (ra, rb, rc) = DFS(curr.borrow_mut().right.take());

                // 状态a：`root`必须放置摄像头的情况下，覆盖整棵树需要的摄像头数目。
                // 状态b：覆盖整棵树需要的摄像头数目，无论`root`是否放置摄像头。
                // 状态c：覆盖两棵子树需要的摄像头数目，无论节点`root`本身是否被监控到。
                let a = lc + rc + 1;
                let b = min(a, min(la + rb, ra + lb));
                let c = min(a, lb + rb);

                (a, b, c)
            }
        };

    DFS(root).1
}

Function<TreeNode, int[]> dfs1 = (root) -> {
    if (root == null) {
        return new int[]{Integer.MAX_VALUE / 2, 0, 0};
    }

    int[] left = this.dfs1.apply(root.left);
    int[] right = this.dfs1.apply(root.right);

    // 状态a：`root`必须放置摄像头的情况下，覆盖整棵树需要的摄像头数目。
    // 状态b：覆盖整棵树需要的摄像头数目，无论`root`是否放置摄像头。
    // 状态c：覆盖两棵子树需要的摄像头数目，无论节点`root`本身是否被监控到。
    int a = left[2] + right[2] + 1;
    int b = Math.min(a, Math.min(left[0] + right[1], right[0] + left[1]));
    int c = Math.min(a, left[1] + right[1]);

    return new int[]{a, b, c};
};

public int minCameraCover(TreeNode root) {
    return this.dfs1.apply(root)[1];
}

func minCameraCover(root *TreeNode) int {
    var dfs func(*TreeNode) (int, int, int)
    dfs = func(root *TreeNode) (int, int, int) {
        if root == nil {
            return math.MaxInt / 2, 0, 0
        }

        la, lb, lc := dfs(root.Left)
        ra, rb, rc := dfs(root.Right)

        // 状态a：`root`必须放置摄像头的情况下，覆盖整棵树需要的摄像头数目。
        // 状态b：覆盖整棵树需要的摄像头数目，无论`root`是否放置摄像头。
        // 状态c：覆盖两棵子树需要的摄像头数目，无论节点`root`本身是否被监控到。
        a := lc + rc + 1
        b := min(a, min(la+rb, ra+lb))
        c := min(a, lb+rb)

        return a, b, c
    }

    _, b, _ := dfs(root)

    return b
}

方法 2: 贪心

pub fn min_camera_cover(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    const DFS: fn(Option<Rc<RefCell<TreeNode>>>, &mut i32) -> i32 = 
        |root, res| match root {
            None => 2,
            Some(curr) => {
                let left = DFS(curr.borrow_mut().left.take(), res);
                let right = DFS(curr.borrow_mut().right.take(), res);

                if left == 2 && right == 2 {
                    return 0;
                }

                if left == 0 || right == 0 {
                    *res += 1;
                    return 1;
                }

                if left == 1 || right == 1 {
                    return 2;
                }

                -1
            }
        };

    let mut res = 0;
    // 0：该节点无覆盖
    // 1：本节点有摄像头
    // 2：本节点有覆盖
    if DFS(root, &mut res) == 0 {
        res += 1;
    }

    res
}

BiFunction<TreeNode, int[], Integer> dfs2 = (root, res) -> {
    if (root == null) {
        return 2;
    }

    int left = this.dfs2.apply(root.left, res);
    int right = this.dfs2.apply(root.right, res);

    if (left == 2 && right == 2) {
        return 0;
    }

    if (left == 0 || right == 0) {
        res[0]++;
        return 1;
    }

    if (left == 1 || right == 1) {
        return 2;
    }

    return -1;
};

public int minCameraCover(TreeNode root) {
    int[] res = new int[]{0};
    // 0：该节点无覆盖
    // 1：本节点有摄像头
    // 2：本节点有覆盖
    if (this.dfs2.apply(root, res) == 0) {
        res[0]++;
    }

    return res[0];
}

func minCameraCover(root *TreeNode) int {
    var dfs func(*TreeNode, *int) int
    dfs = func(root *TreeNode, res *int) int {
        if root == nil {
            return 2
        }

        left := dfs(root.Left, res)
        right := dfs(root.Right, res)

        if left == 2 && right == 2 {
            return 0
        }

        if left == 0 || right == 0 {
            *res++
            return 1
        }

        if left == 1 || right == 1 {
            return 2
        }

        return -1
    }

    res := 0
    // 0：该节点无覆盖
    // 1：本节点有摄像头
    // 2：本节点有覆盖
    if dfs(root, &res) == 0 {
    	res++
    }

    return res
}