51, N皇后

一、题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n皇后问题研究的是如何将n个皇后放置在n×n的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数n，返回所有不同的n皇后问题的解决方案。

每一种解法包含一个不同的n皇后问题的棋子放置方案，该方案中'Q'和'.'分别代表了皇后和空位。

示例 1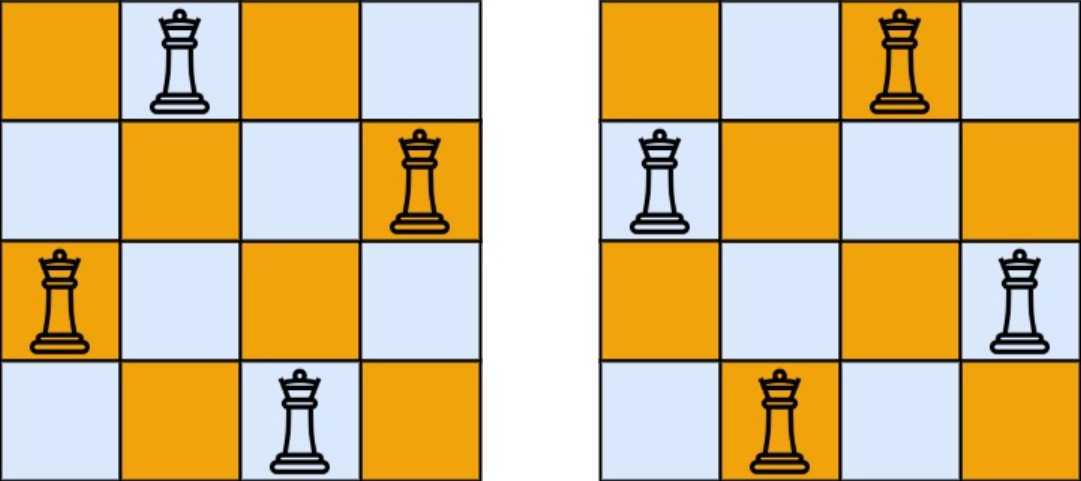

输入: n = 4
输出: [[".Q..", "...Q", "Q...", "..Q."],["..Q.", "Q...", "...Q", ".Q.."]]
解释: 如上图所示，4皇后问题存在两个不同的解法。

示例 2
输入: n = 1
输出: [["Q"]]

提示

• 1 <= n <= 9

相关主题

• 数组
• 回溯

二、题解

方法 1: 回溯

pub fn solve_n_queens(n: i32) -> Vec<Vec<String>> {
    const DFS: fn(i32, i32, &mut Vec<(i32, i32)>, &mut Vec<Vec<String>>) =
        |row, len, pos, res| {
            if row == len {
                let ans = pos
                    .iter()
                    .map(|&(_, col)| {
                        (0..len).into_iter().fold(
                            String::with_capacity(len as usize),
                            |mut str, c| {
                                if c == col {
                                    str.push('Q');
                                } else {
                                    str.push('.');
                                }
                                str
                            },
                        )
                    })
                    .collect::<Vec<_>>();

                res.push(ans);

                return;
            }

            for col in 0..len {
                if pos.iter().any(|&(r, c)| {
                    // 同一列
                    if col == c {
                        return true;
                    }

                    let slope = (row - r) as f64 / (col - c) as f64;
                    // 同一对角线
                    slope == 1.0 || slope == -1.0
                }) {
                    continue;
                }

                pos.push((row, col));
                DFS(row + 1, len, pos, res);
                pos.pop();
            }
        };
    let mut res = vec![];

    DFS(0, n, &mut vec![], &mut res);

    res
}

@FunctionalInterface
interface QuadrConsumer<A, B, C, D> {
    void accept(A a, B b, C c, D d);
}

QuadrConsumer<Integer, Integer, List<int[]>, List<List<String>>> dfs =
        (row, len, pos, res) -> {
            if (Objects.equals(row, len)) {
                List<String> ans = pos.stream().map(p -> {
                    StringBuilder s = new StringBuilder(len);
                    for (int c = 0; c < len; c++) {
                        if (c == p[1]) {
                            s.append('Q');
                        } else {
                            s.append('.');
                        }
                    }
                    return s.toString();
                }).collect(Collectors.toList());

                res.add(ans);

                return;
            }

            for (int col = 0; col < len; col++) {
                int finalCol = col;
                if (pos.stream().anyMatch(p -> {
                    // 同一列
                    if (p[1] == finalCol) {
                        return true;
                    }

                    double slope = ((double) (row - p[0])) / (finalCol - p[1]);
                    // 同一对角线
                    return slope == 1 || slope == -1;
                })) {
                    continue;
                }

                pos.addLast(new int[]{row, col});
                this.dfs.accept(row + 1, len, pos, res);
                pos.removeLast();
            }
        };

public List<List<String>> solveNQueens(int n) {
    List<List<String>> res = new ArrayList<>();

    this.dfs.accept(0, n, new ArrayList<>(), res);

    return res;
}