二叉树

Mike大约 7 分钟

二叉树

定义

在计算机科学中，二叉树open in new window是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构。通常分支被称作左子树或右子树。二叉树的分支具有左右次序，不能随意颠倒。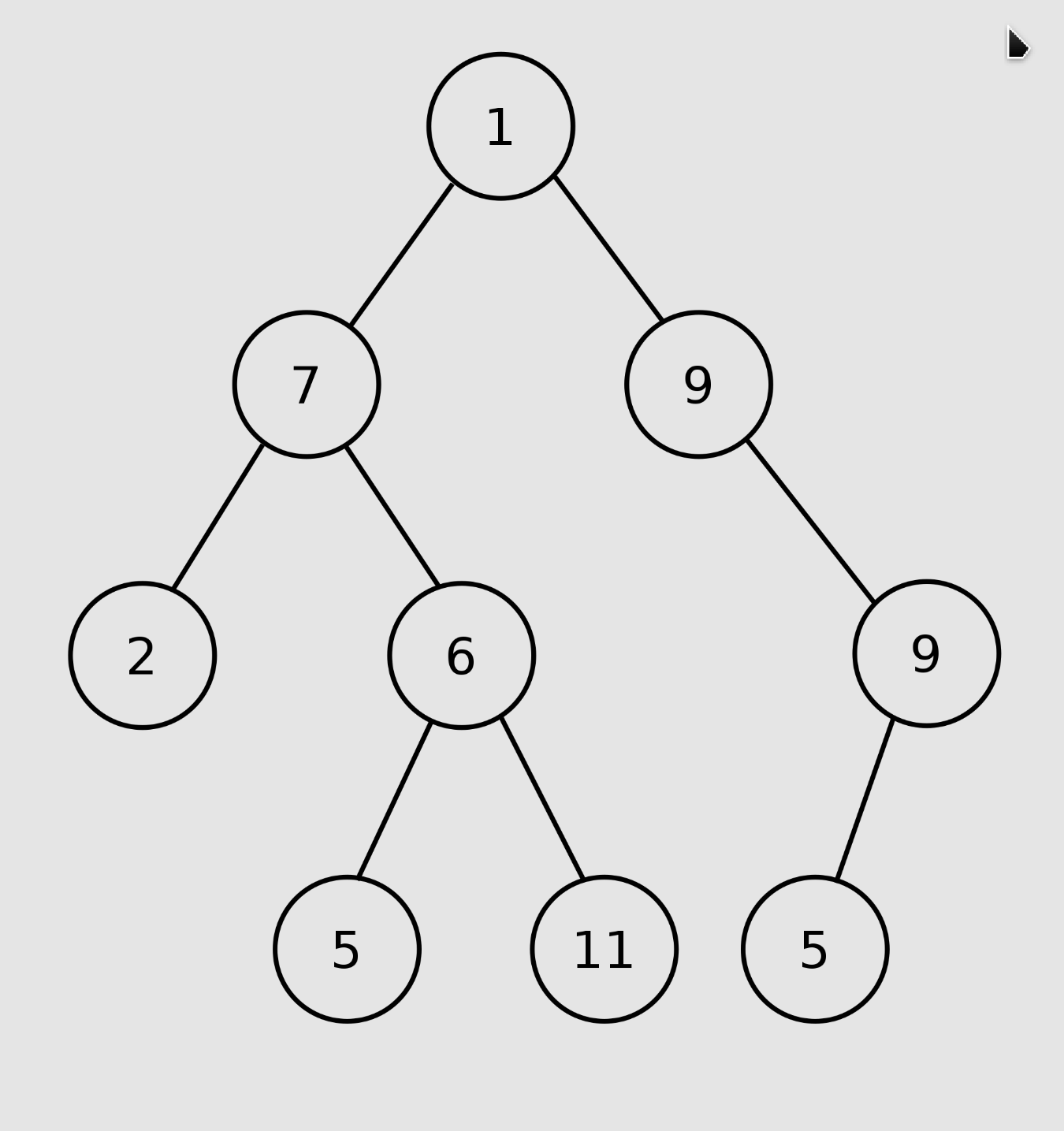
binary_tree

在图论中的定义

二叉树是一个连通的无环图，并且每一个顶点的度不大于3。有根二叉树还要满足根节点的度不大于2。有了根节点之后，每个顶点定义了唯一的父节点，和最多2个子节点。然而，没有足够的信息来区分左节点和右节点。如果不考虑连通性，允许图中有多个连通分量，这样的结构叫做森林。

二叉树的类型

满二叉树：每个节点要么有0个孩子节点要么有2个孩子节点的二叉树，称为满二叉树。
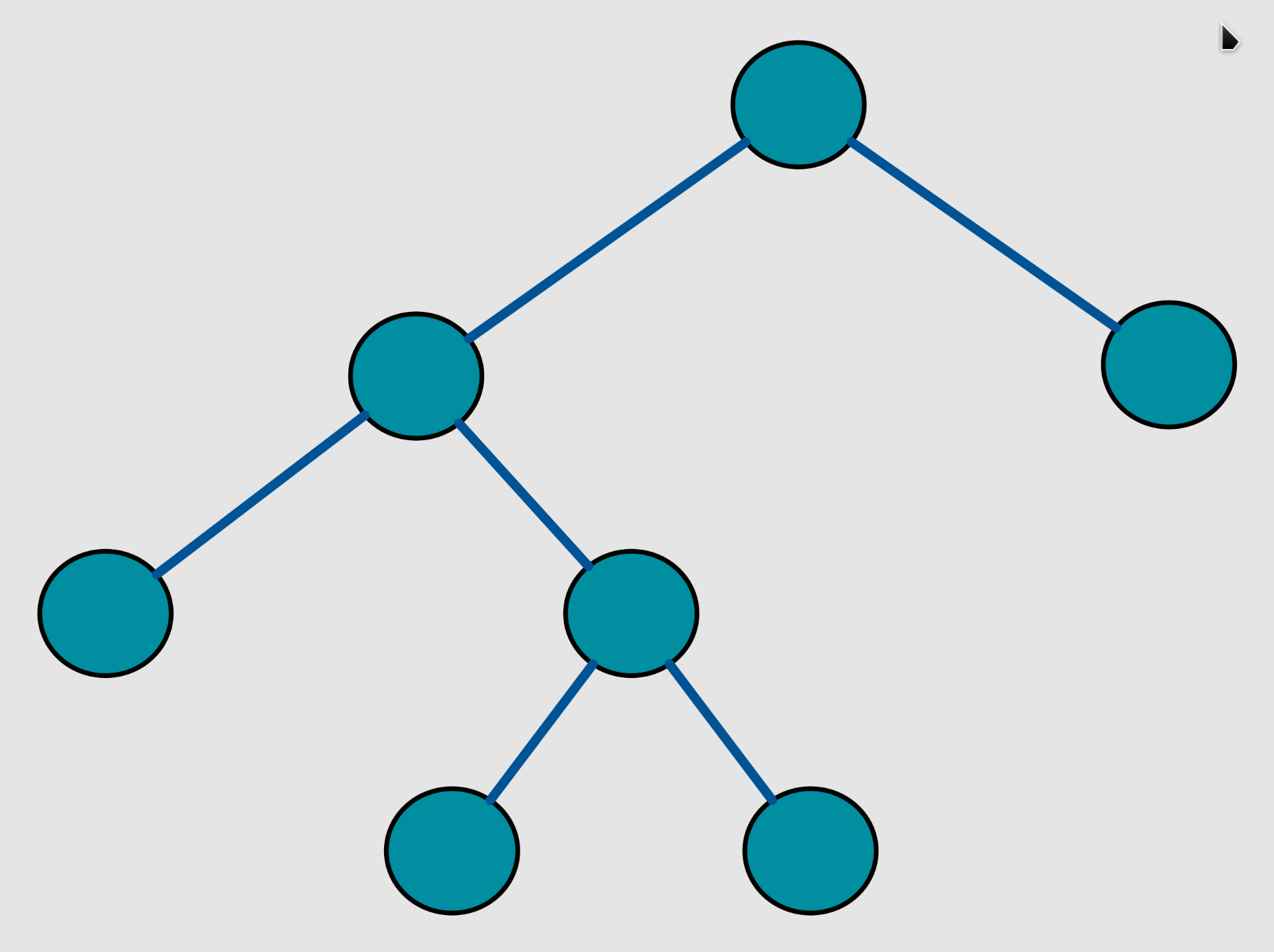
完美二叉树：一棵深度为k，且有2^k − 1个节点的二叉树，称为完美二叉树。这种树的特点是每一层上的节点数都是最大节点数。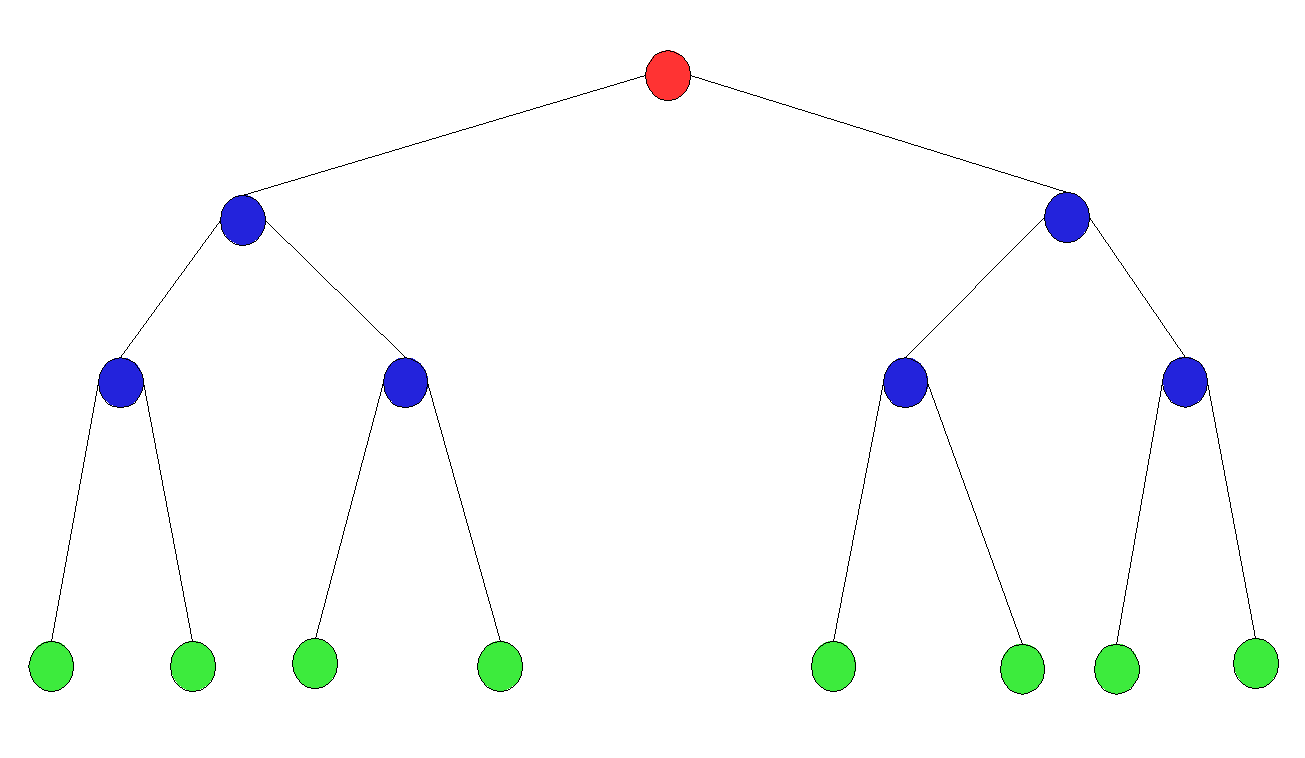
完全二叉树：在一颗二叉树中，若除最后一层外的其余层都是满的，并且最后一层要么是满的，要么在右边缺少连续若干节点，则此二叉树为完全二叉树。
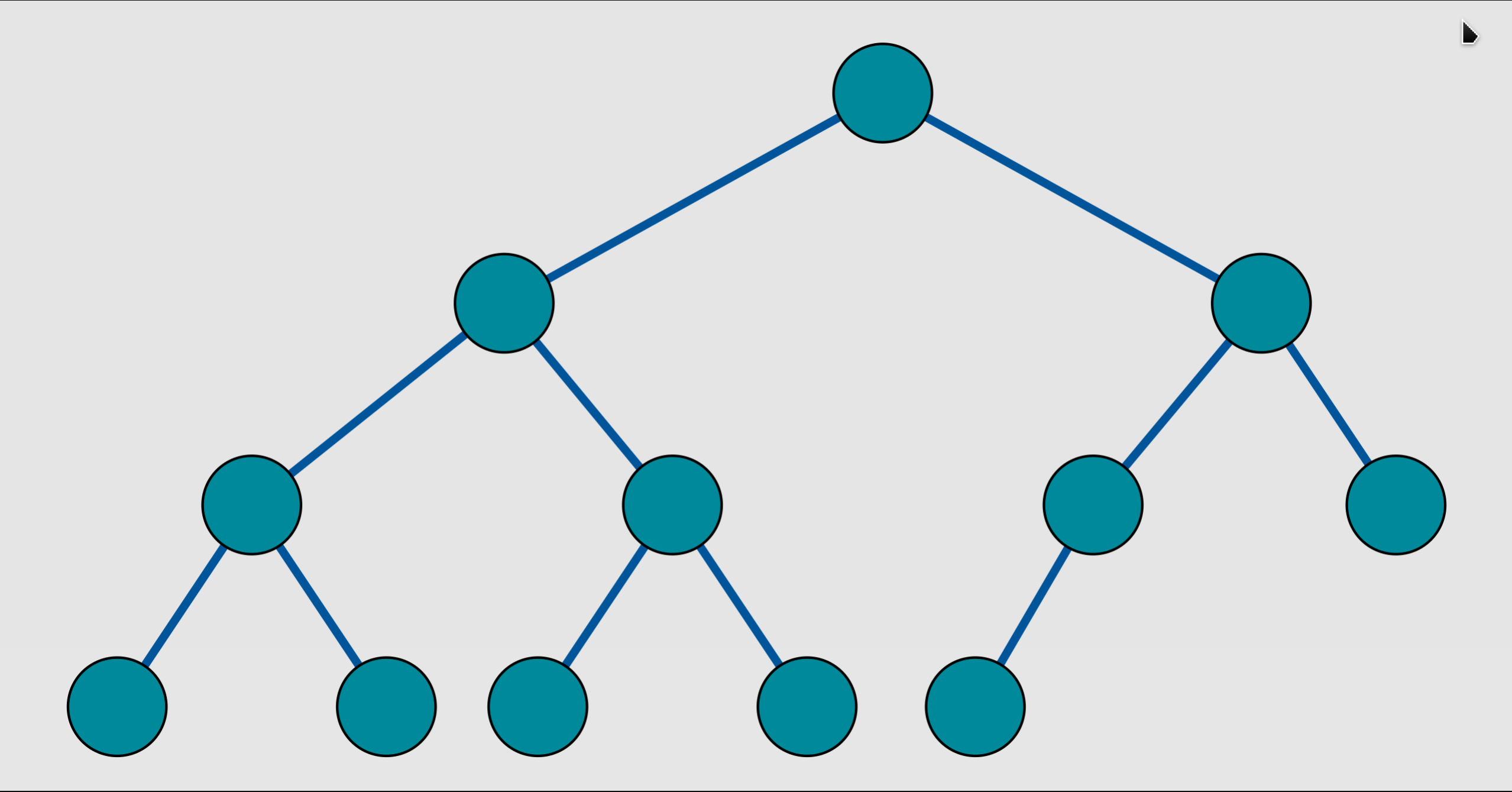
退化二叉树：许多节点只有1个孩子节点，其行为表现更像是单链表的二叉树。
二叉搜索树open in new window：又称二叉查找树、有序二叉树或排序二叉树，是指一棵空树或者具有下列性质的二叉树：
- 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
- 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
- 任意节点的左、右子树也分别为二叉搜索树；
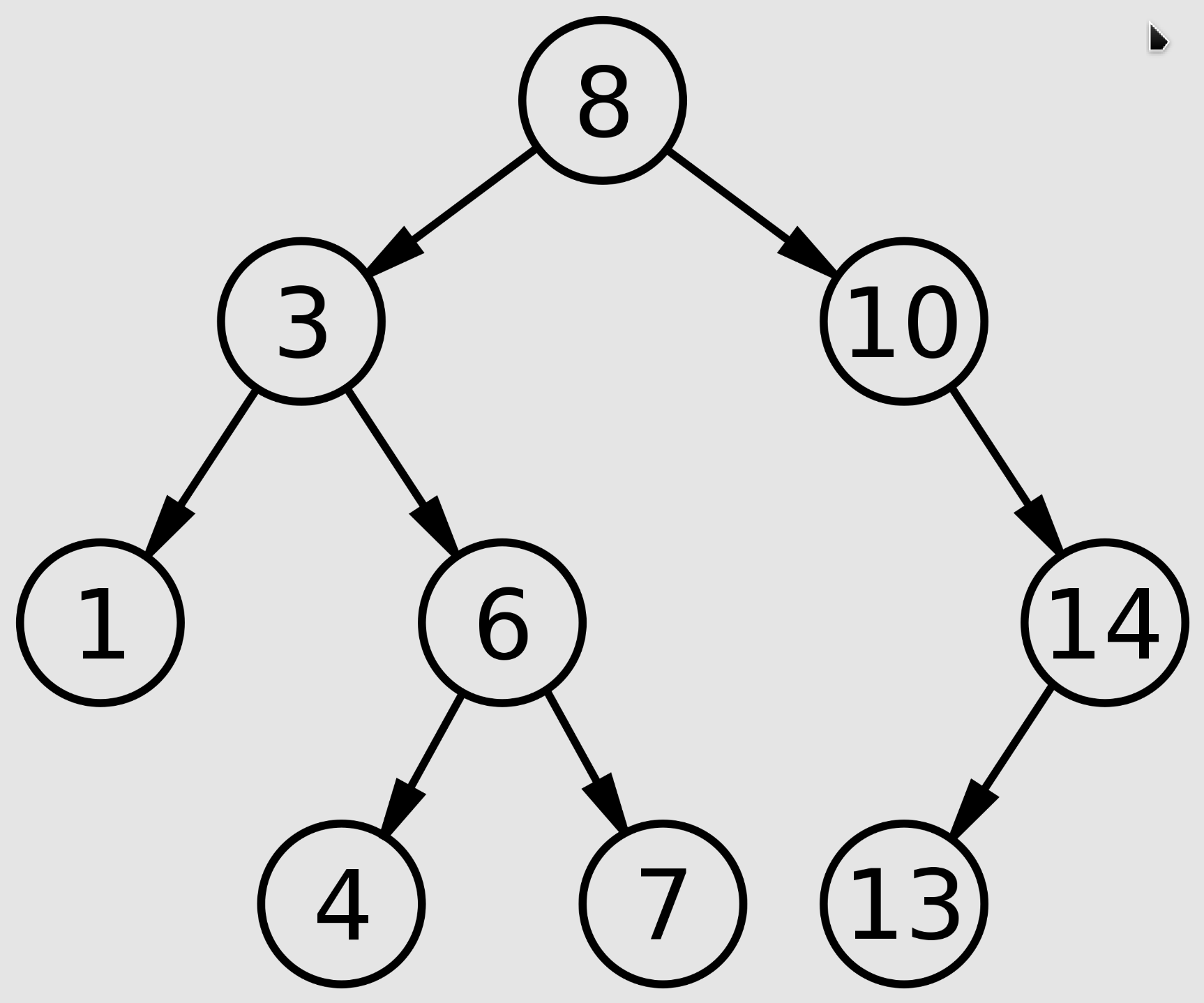
AVLopen in new window：AVL树（Adelson-Velsky and Landis Tree）是计算机科学中最早被发明的自平衡二叉搜索树。在AVL树中，任一节点对应的两棵子树的最大高度差为1，因此它也被称为高度平衡树。
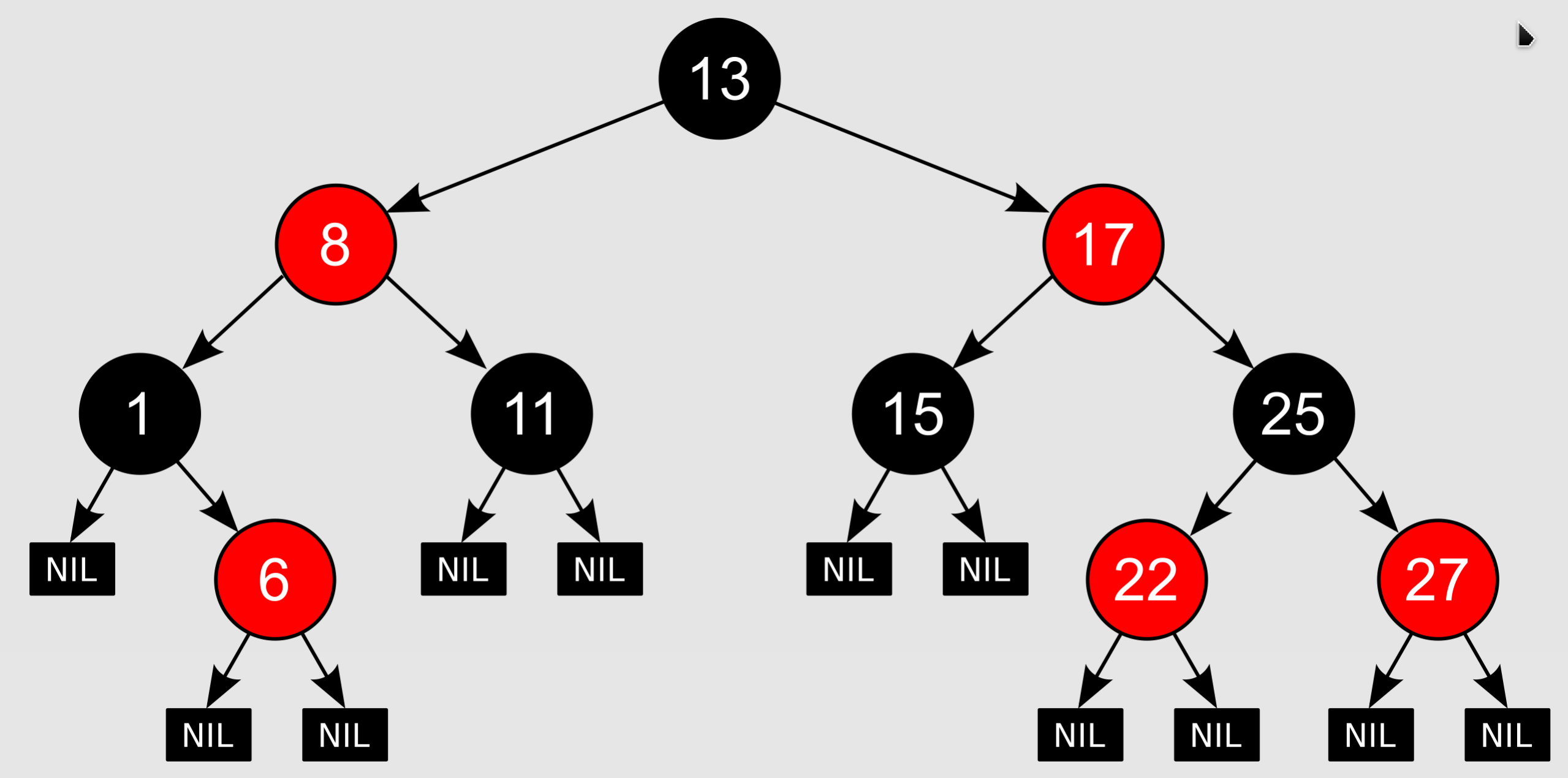
红黑树open in new window：红黑树（Red–black tree）是每个节点都带有颜色属性的一种自平衡二叉搜索树，其有以下额外要求：
- 节点是红色或黑色；
- 根是黑色；
- 所有叶子都是黑色（叶子是NIL节点）；
- 每个红色节点必须有两个黑色的子节点；
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点；

二叉树的性质

对于高度为h的满二叉树，其节点总数n和h的关系为2h + 1 <= n <= 2^(h+1) - 1。根节点的高度为0。对于一颗完美二叉树，其节点总数为1 + 2 + 4 + … + 2^ℎ = 2^(ℎ+1) − 1。
对于有n个节点的完美二叉树，其叶子节点个数为l = (n + 1) / 2。
对于任意一颗非空二叉树，其叶子节点个数l与度为2的内部节点个数i2的关系为l = i2 + 1。
对于有n个节点的二叉树，其最小的树高为ℎ = log2(n + 1) − 1，此时二叉树表现为完全二叉树。
对于有l个叶子节点的二叉树，其高度至少是ℎ = log2(l)。
对于一颗节点总数为n、边总数为e的非空二叉树，则节点总数与边的关系为e = n - 1。
对于一颗节点总数为n的二叉树，其缺失的孩子节点总数为n + 1。
对于有n个节点的完全二叉树，其内部节点的个数为⌊n/2⌋。

二叉树的操作

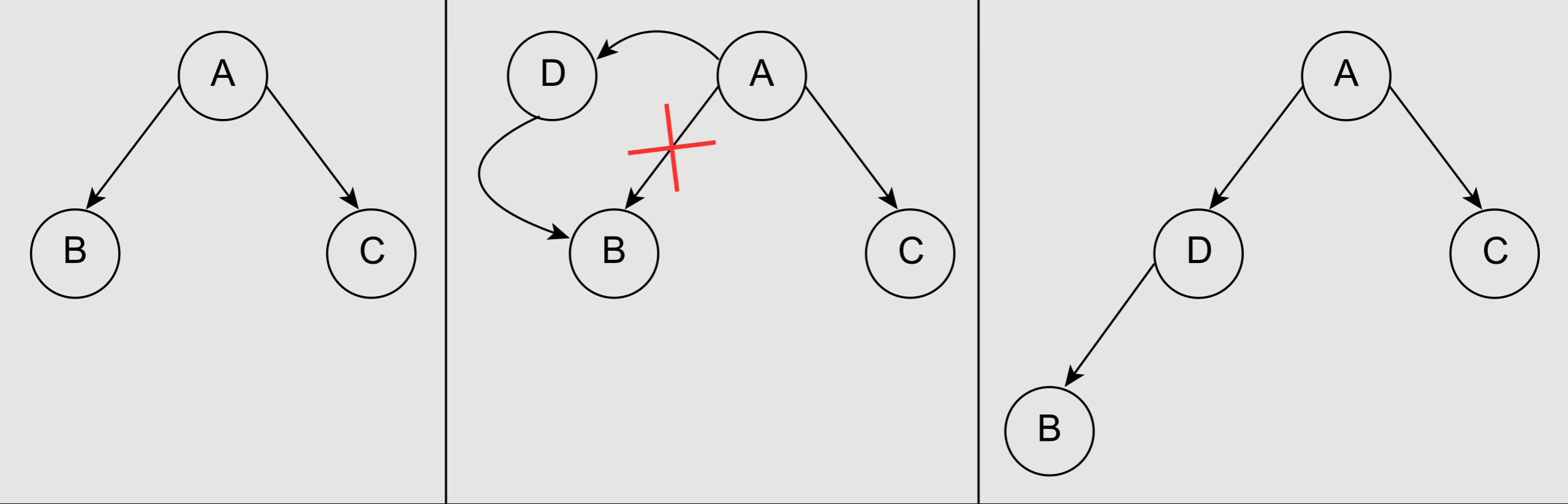
插入

叶子节点
内部节点

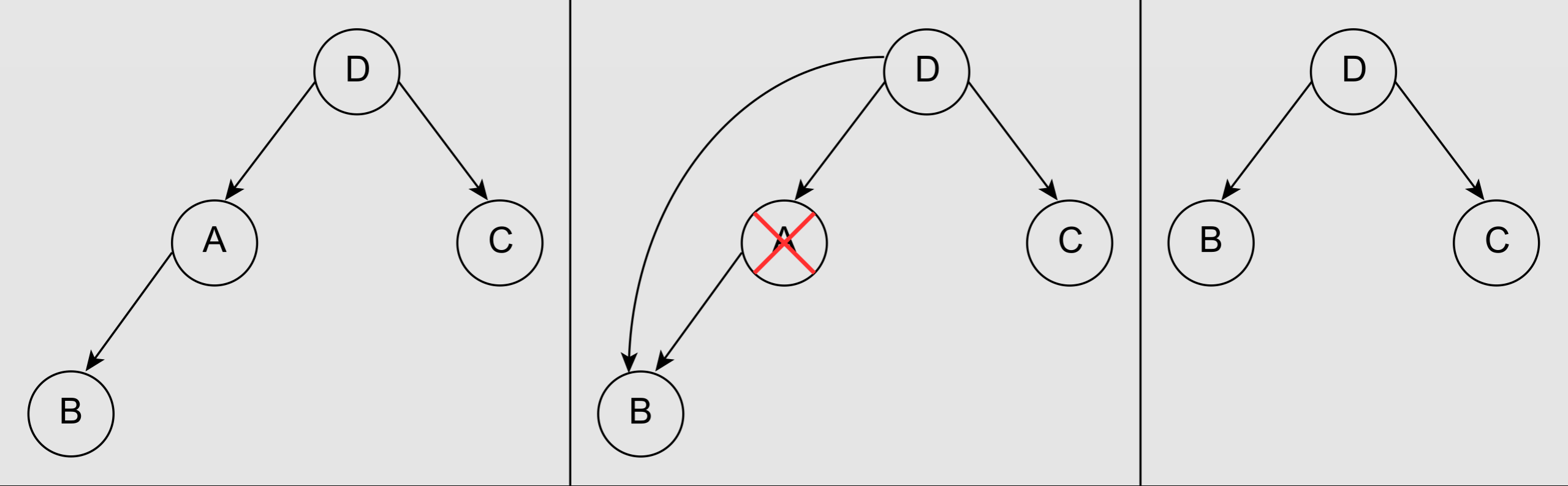
删除

无孩子节点或有1个孩子节点的节点
有2个孩子节点的节点

遍历

深度优先遍历（DFS）

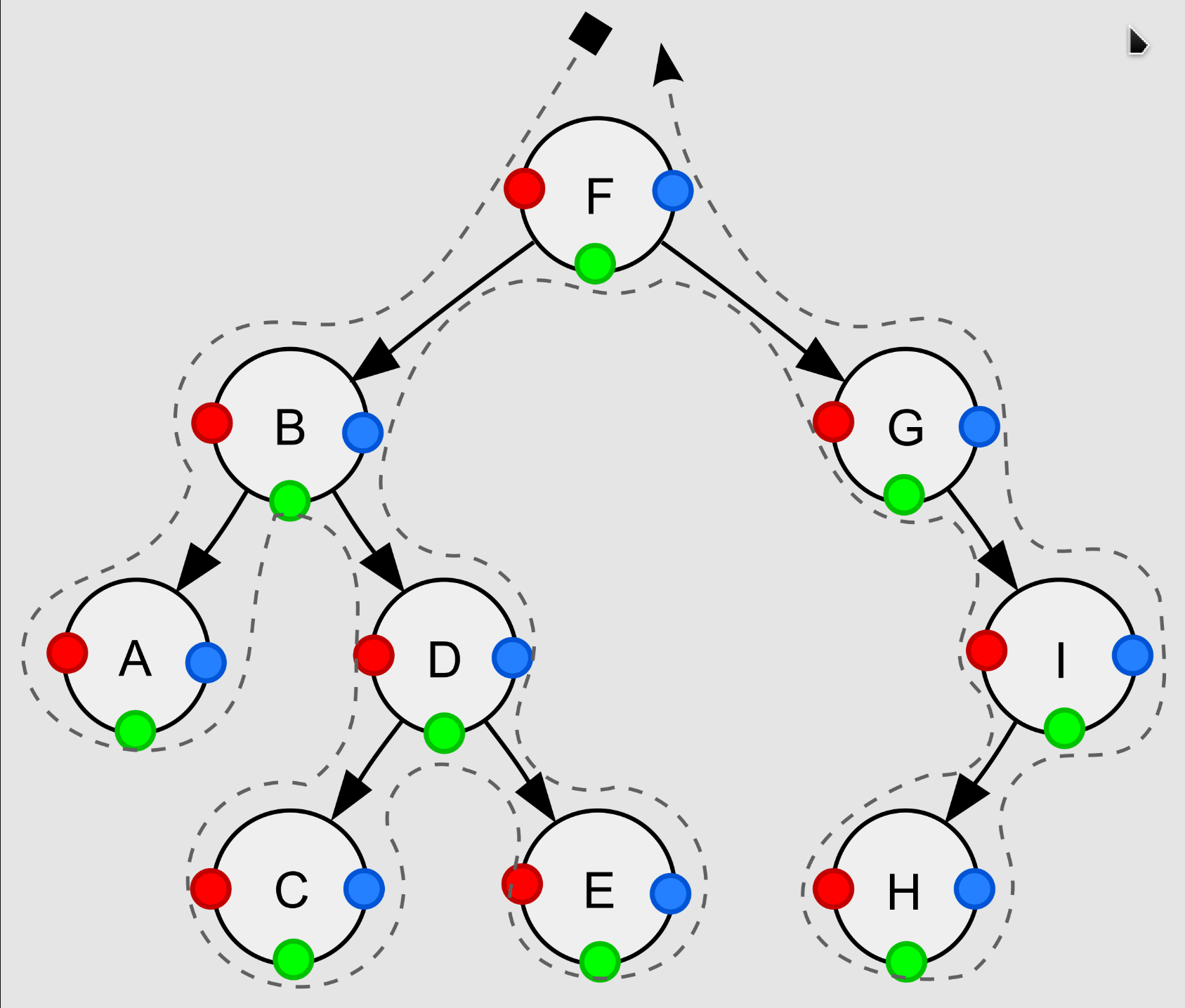
前序遍历(根左右), 红色●表示其访问顺序: F, B, A, D, C, E, G, I, H

procedure pre_order(node)
    if node = null
        return
    visit(node)
    pre_order(node.left)
    pre_order(node.right)

procedure pre_order(node)
    if node = null
        return
    stack ← empty stack
    stack.push(node)
    while not stack.isEmpty()
        node ← stack.pop()
        visit(node)
        // right child is pushed first so that left is processed first
        if node.right ≠ null
            stack.push(node.right)
        if node.left ≠ null
            stack.push(node.left)

中序遍历(左根右), 绿色●表示其访问顺序: A, B, C, D, E, F, G, H, I

procedure in_order(node)
    if node = null
        return
    in_order(node.left)
    visit(node)
    in_order(node.right)

procedure in_order(node)
    stack ← empty stack
    while not stack.isEmpty() or node ≠ null
        if node ≠ null
            stack.push(node)
            node ← node.left
        else
            node ← stack.pop()
            visit(node)
            node ← node.right

后序遍历(左右根), 蓝色●表示其访问顺序: A, C, E, D, B, H, I, G, F

procedure post_order(node)
    if node = null
        return
    post_order(node.left)
    post_order(node.right)
    visit(node)

procedure post_order(node)
    stack ← empty stack
    lastNodeVisited ← null
    while not stack.isEmpty() or node ≠ null
        if node ≠ null
            stack.push(node)
            node ← node.left
        else
            peekNode ← stack.peek()
            // if right child exists and traversing node
            // from left child, then move right
            if peekNode.right ≠ null and lastNodeVisited ≠ peekNode.right
                node ← peekNode.right
            else
                visit(peekNode)
                lastNodeVisited ← stack.pop()

广度优先遍历（BFS）

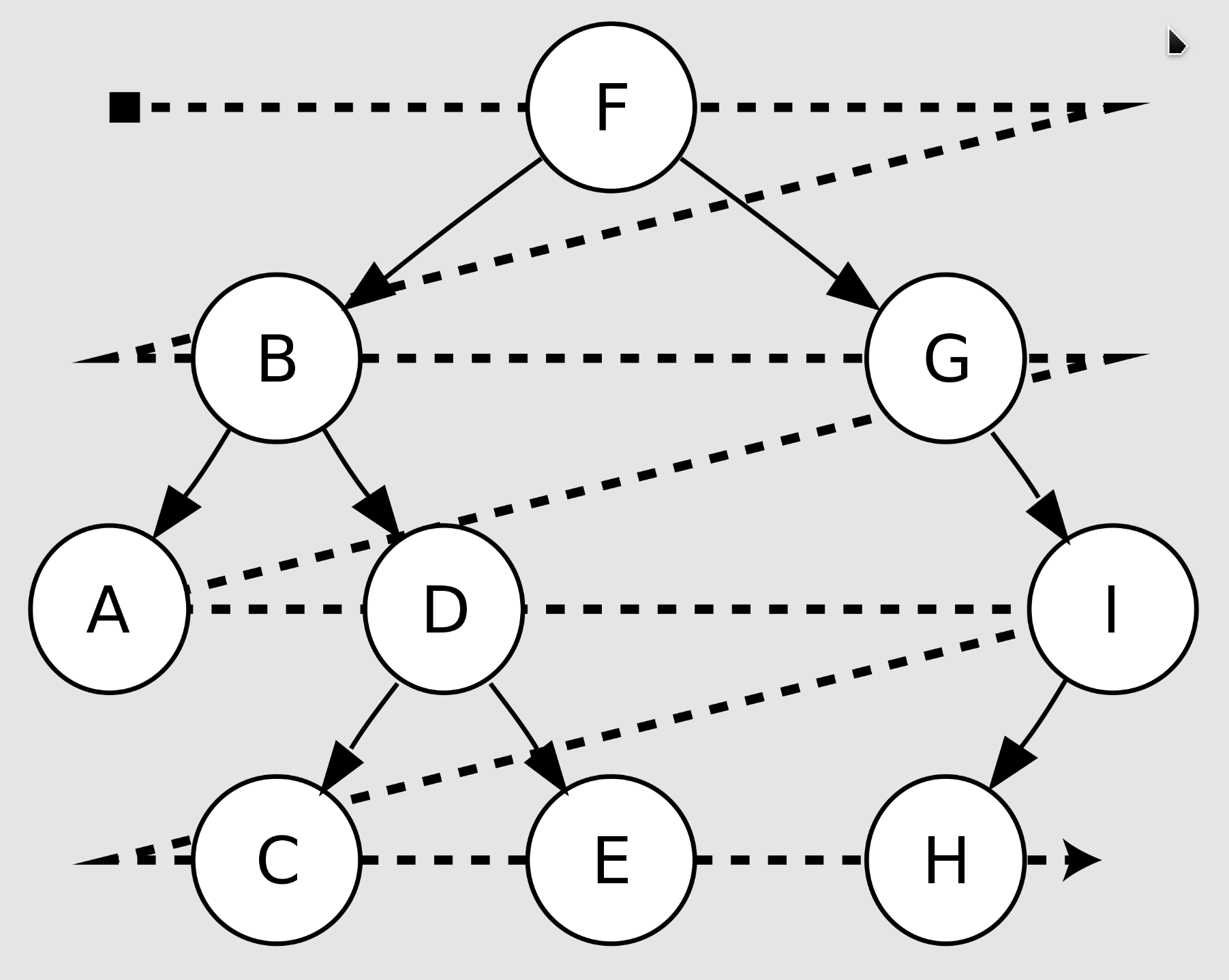
层序遍历: F, B, G, A, D, I, C, E, H

procedure level_order(node)
    queue ← empty queue
    queue.enqueue(node)
    while not queue.isEmpty()
        node ← queue.dequeue()
        visit(node)
        if node.left ≠ null
            queue.enqueue(node.left)
        if node.right ≠ null
            queue.enqueue(node.right)

复杂度

时间复杂度

Operation	Average	Worst case
Search	O(log(n))	O(n)
Insert	O(log(n))	O(n)
Delete	O(log(n))	O(n)

空间复杂度

Operation	Average	Worst case
Space	O(n)	O(n)

习题

二叉树

# 二叉树

# 定义

# 在图论中的定义

# 二叉树的类型

# 二叉树的性质

# 二叉树的操作

# 插入

# 删除

# 遍历

# 深度优先遍历（DFS）

# 广度优先遍历（BFS）

# 复杂度

# 时间复杂度

# 空间复杂度

# 习题

# 二叉树的遍历方式

# 二叉树的层序遍历

# 二叉树的属性

# 二叉树的修改与构造

# 二叉搜索树的属性

# 二叉树公共祖先问题

# 二叉搜索树的修改与构造

# 其他

# 总结

二叉树

定义

在图论中的定义

二叉树的类型

二叉树的性质

二叉树的操作

插入

删除

遍历

深度优先遍历（DFS）

广度优先遍历（BFS）

复杂度

时间复杂度

空间复杂度

习题

二叉树的遍历方式

二叉树的层序遍历

二叉树的属性

二叉树的修改与构造

二叉搜索树的属性

二叉树公共祖先问题

二叉搜索树的修改与构造

其他

总结