501, 二叉搜索树中的众数

一、题目描述

给你一个含重复值的二叉搜索树（BST）的根节点root，找出并返回BST中的所有众数（即出现频率最高的元素）。

如果树中有不止一个众数，可以按任意顺序返回。

假定BST满足如下定义：

• 结点左子树中所含节点的值小于等于当前节点的值
• 结点右子树中所含节点的值大于等于当前节点的值
• 左子树和右子树都是二叉搜索树

示例 1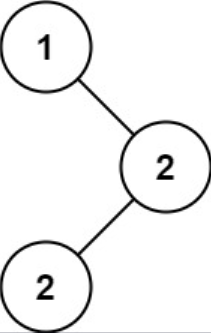

输入: root = [1, null, 2, 2]
输出: [2]

示例 2
输入: root = [0]
输出: [0]

提示

• 树中节点的数目在范围[1, 10⁴]内
• -10⁵ <= Node.val <= 10⁵

进阶
你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

相关主题

• 树
• 深度优先搜索
• 二叉搜索树
• 二叉树

二、题解

#[derive(Debug, PartialEq, Eq)]
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Rc<RefCell<TreeNode>>>,
    pub right: Option<Rc<RefCell<TreeNode>>>,
}

impl TreeNode {
    #[inline]
    pub fn new(val: i32) -> Self {
        TreeNode {
            val,
            left: None,
            right: None,
        }
    }
}

///       val: 正在遍历的节点的值
///  curr_val: 当前节点的值（当前值）
/// curr_freq: 当前值出现的频率
///  max_freq: 频率的最大值
///       res: 最终生成的结果
fn update(val: i32, curr_val: &mut i32, curr_freq: &mut usize, max_freq: &mut usize, res: &mut Vec<i32>) {
    if val == *curr_val {
        *curr_freq += 1;
    } else {
        *curr_val = val;
        *curr_freq = 1;
    }
    if *curr_freq > *max_freq {
        res.clear();
        *max_freq = *curr_freq;
    }
    if *curr_freq == *max_freq {
        res.push(val);
    }
}

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

/**
 * val: 正在遍历的节点的值
 * params:
 *   0: 当前节点的值（当前值）
 *   1: 当前值出现的频率
 *   2: 频率的最大值
 * res: 最终生成的结果
 */
TriConsumer<Integer, int[], List<Integer>> update = (val, params, res) -> {
    if (val == params[0]) {
        params[1]++;
    } else {
        params[0] = val;
        params[1] = 1;
    }
    if (params[1] > params[2]) {
        res.clear();
        params[2] = params[1];
    }
    if (params[1] == params[2]) {
        res.add(val);
    }
};

方法 1: 使用哈希表

pub fn find_mode(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
    //Self::use_hashmap_recur(root)
    Self::use_hashmap_iter(root)
}

///
/// Time complexity: O(n)
/// Space complexity: O(n)
///
fn use_hashmap_recur(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
    let mut map = HashMap::new();
    const PREORDER: fn(Option<Rc<RefCell<TreeNode>>>, &mut HashMap<i32, usize>) =
        |root, counter| {
            if let Some(curr) = root {
                let curr_val = curr.borrow().val;
                counter
                    .entry(curr_val)
                    .and_modify(|count| *count += 1)
                    .or_insert(1);
                PREORDER(curr.borrow_mut().left.take(), counter);
                PREORDER(curr.borrow_mut().right.take(), counter);
            }
        };

    PREORDER(root, &mut map);

    let max_freq = map.values().max().map(|v| *v).unwrap_or_default();
    map.into_iter()
        .filter_map(|(k, v)| {
            if v == max_freq {
                return Some(k);
            }
            None
        })
        .collect()
}

///
/// Time complexity: O(n)
/// Space complexity: O(n)
///
fn use_hashmap_iter(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
    let mut map = HashMap::new();

    if let Some(root) = root {
        let mut stack = vec![root];
        while let Some(curr) = stack.pop() {
            let curr_val = curr.borrow().val;
            map.entry(curr_val)
                .and_modify(|count| *count += 1)
                .or_insert(1);

            if let Some(right) = curr.borrow_mut().right.take() {
                stack.push(right);
            }
            if let Some(left) = curr.borrow_mut().left.take() {
                stack.push(left);
            }
        }
    }

    let max_freq = map.values().max().map(|v| *v).unwrap_or_default();
    map.into_iter()
        .filter_map(|(k, v)| {
            if v == max_freq {
                return Some(k);
            }
            None
        })
        .collect()
}

public int[] findMode(TreeNode root) {
    //return this.useHashmapRecur(root);
    return this.useHashmapIter(root);
}

BiConsumer<TreeNode, Map<Integer, Integer>> preorder = (root, counter) -> {
    if (root == null) {
        return;
    }

    counter.put(root.val, counter.getOrDefault(root.val, 0) + 1);

    this.preorder.accept(root.left, counter);
    this.preorder.accept(root.right, counter);
};
/**
 * Time complexity: O(n)
 * Space complexity: O(n)
 */
int[] useHashmapRecur(TreeNode root) {
    Map<Integer, Integer> counter = new HashMap<>();

    this.preorder.accept(root, counter);

    Integer maxFreq = counter.values().stream().max(Comparator.naturalOrder()).orElse(0);
    return counter.entrySet().stream()
            .filter(e -> Objects.equals(e.getValue(), maxFreq))
            .map(Map.Entry::getKey).mapToInt(Integer::intValue)
            .toArray();
}


/**
 * Time complexity: O(n)
 * Space complexity: O(n)
 */
int[] useHashmapIter(TreeNode root) {
    Map<Integer, Integer> counter = new HashMap<>();

    if (root != null) {
        Deque<TreeNode> stack = new ArrayDeque<>() {{
            this.push(root);
        }};

        while (!stack.isEmpty()) {
            TreeNode curr = stack.pop();
            counter.put(curr.val, counter.getOrDefault(curr.val, 0) + 1);

            if (curr.right != null) {
                stack.push(curr.right);
            }
            if (curr.left != null) {
                stack.push(curr.left);
            }
        }
    }

    Integer maxFreq = counter.values().stream().max(Comparator.naturalOrder()).orElse(0);
    return counter.entrySet().stream()
            .filter(e -> Objects.equals(e.getValue(), maxFreq))
            .map(Map.Entry::getKey).mapToInt(Integer::intValue)
            .toArray();
}

方法 2: 中序遍历

pub fn find_mode(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
    //Self::in_order_traversal_recur(root)
    Self::in_order_traversal_iter(root)
}

///
/// Time complexity: O(n)
/// Space complexity: O(n)
///
fn in_order_traversal_recur(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
    let mut res = vec![];
    let mut curr_val = i32::MIN;
    let mut curr_freq = 0;
    let mut max_freq = 0;
    const INORDER: fn(Option<Rc<RefCell<TreeNode>>>, &mut i32, &mut usize, &mut usize, &mut Vec<i32>) = 
        |root, curr_val, curr_freq, max_freq, res| {
            if let Some(curr) = root {
                INORDER(curr.borrow_mut().left.take(), curr_val, curr_freq, max_freq, res);
                
                let val = curr.borrow().val;
                Solution::update(val, curr_val, curr_freq, max_freq, res);
                
                INORDER(curr.borrow_mut().right.take(), curr_val, curr_freq, max_freq, res);
            }
    };

    INORDER(root, &mut curr_val, &mut curr_freq, &mut max_freq, &mut res);

    res
}

///
/// Time complexity: O(n)
/// Space complexity: O(n)
///
fn in_order_traversal_iter(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
    let mut res = vec![];

    if let Some(root) = root {
        let mut curr_val = i32::MIN;
        let mut curr_freq = 0;
        let mut max_freq = 0;
        let mut stack = vec![Ok(root)];

        while let Some(curr) = stack.pop() {
            match curr {
                Ok(node) => {
                    if let Some(right) = node.borrow_mut().right.take() {
                        stack.push(Ok(right));
                    }

                    stack.push(Err(node.borrow().val));

                    if let Some(left) = node.borrow_mut().left.take() {
                        stack.push(Ok(left));
                    }
                }
                Err(val) => {
                    Solution::update(val, &mut curr_val, &mut curr_freq, &mut max_freq, &mut res);
                }
            }
        }
    }

    res
}

public int[] findMode(TreeNode root) {
    //return this.inorderTraversalRecur(root);
    return this.inorderTraversalIter(root);
}

@FunctionalInterface
interface TriConsumer<A, B, C> {
    void accept(A a, B b, C c);
}

TriConsumer<TreeNode, int[], List<Integer>> inorder = (root, params, res) -> {
    if (root == null) {
        return;
    }
    this.inorder.accept(root.left, params, res);

    this.update.accept(root.val, params, res);

    this.inorder.accept(root.right, params, res);
};

/**
 * Time complexity: O(n)
 * Space complexity: O(n)
 */
int[] inorderTraversalRecur(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    int[] params = {Integer.MIN_VALUE, 0, 0};

    this.inorder.accept(root, params, res);

    return res.stream().mapToInt(Integer::intValue).toArray();
}

/**
 * Time complexity: O(n)
 * Space complexity: O(n)
 */
int[] inorderTraversalIter(TreeNode root) {
    List<Integer> res = new ArrayList<>();

    if (root != null) {
        int[] params = new int[]{Integer.MIN_VALUE, 0, 0};
        Deque<Object> stack = new ArrayDeque<>() {{
            this.push(root);
        }};

        while (!stack.isEmpty()) {
            Object obj = stack.pop();
            switch (obj) {
                case TreeNode curr -> {
                    if (curr.right != null) {
                        stack.push(curr.right);
                    }

                    stack.push(curr.val);

                    if (curr.left != null) {
                        stack.push(curr.left);
                    }
                }
                case Integer val -> {
                    this.update.accept(val, params, res);
                }
                default -> throw new IllegalStateException("Unexpected value: " + obj);
            }
        }
    }

    return res.stream().mapToInt(Integer::intValue).toArray();
}

方法 3: Morris中序遍历

pub fn find_mode(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
    //Self::morris_in_order_iter_1(root)
    Self::morris_in_order_iter_2(root)
}

///
/// Time complexity: O(n)
/// Space complexity: O(1)
///
fn morris_in_order_iter_1(mut root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
    let mut res = vec![];
    let mut curr_val = i32::MIN;
    let mut curr_freq = 0;
    let mut max_freq = 0;

    while let Some(curr) = root {
        let val = curr.borrow().val;
        let left = curr.borrow().left.clone();

        if left.is_some() {
            let mut prev_node = left.clone();

            while let Some(ref prev) = prev_node {
                let right = prev.borrow().right.clone();
                if right.is_none() || right == Some(curr.clone()) {
                    break;
                } else {
                    prev_node = right;
                }
            }

            match prev_node {
                None => break, // this is mark code
                Some(prev) => {
                    let mut prev = prev.borrow_mut();

                    if let Some(_) = prev.right.take() {
                        Solution::update(val, &mut curr_val, &mut curr_freq, &mut max_freq, &mut res);
                        root = curr.borrow().right.clone();
                    } else {
                        prev.right = Some(curr);
                        root = left;
                    }
                }
            }
        } else {
            Solution::update(val, &mut curr_val, &mut curr_freq, &mut max_freq, &mut res);
            root = curr.borrow().right.clone();
        };
    }

    res
}

///
/// Time complexity: O(n)
/// Space complexity: O(1)
///
fn morris_in_order_iter_2(mut root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
    let mut res = vec![];
    let mut curr_val = i32::MIN;
    let mut curr_freq = 0;
    let mut max_freq = 0;

    while let Some(curr) = root {
        let left = curr.borrow().left.clone();
        let val = curr.borrow().val;

        if left.is_none() {
            Solution::update(val, &mut curr_val, &mut curr_freq, &mut max_freq, &mut res);
            root = curr.borrow().right.clone();
            continue;
        }

        let mut prev_node = left.clone();
        while let Some(ref prev) = prev_node {
            let right = prev.borrow().right.clone();
            if right.is_none() || right == Some(curr.clone()) {
                break;
            } else {
                prev_node = right;
            }
        }

        if let Some(prev) = prev_node {
            let mut prev = prev.borrow_mut();
            
            if let Some(_) = prev.right.take() {
                Solution::update(val, &mut curr_val, &mut curr_freq, &mut max_freq, &mut res);
                root = curr.borrow().right.clone();
            } else {
                prev.right = Some(curr);
                root = left;
            }
        } else {
            // here is mark code
            //root = None;
            break;
        }
    }

    res
}

public int[] findMode(TreeNode root) {
    //return this.morrisInorderIter1(root);
    return this.morrisInorderIter2(root);
}

/**
 * Time complexity: O(n)
 * Space complexity: O(1)
 */
int[] morrisInorderIter1(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    int[] params = new int[]{Integer.MIN_VALUE, 0, 0};
    TreeNode prev = null;

    while (root != null) {
        if (root.left != null) {
            prev = root.left;

            while (prev.right != null && prev.right != root) {
                prev = prev.right;
            }

            if (prev.right == null) {
                prev.right = root;
                root = root.left;
            } else {
                prev.right = null;
                this.update.accept(root.val, params, res);
                root = root.right;
            }
        } else {
            this.update.accept(root.val, params, res);
            root = root.right;
        }
    }

    return res.stream().mapToInt(Integer::intValue).toArray();
}

/**
 * Time complexity: O(n)
 * Space complexity: O(1)
 */
int[] morrisInorderIter2(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    int[] params = new int[]{Integer.MIN_VALUE, 0, 0};
    TreeNode prev = null;

    while (root != null) {
        if (root.left == null) {
            this.update.accept(root.val, params, res);
            root = root.right;
            continue;
        }

        prev = root.left;
        while (prev.right != null && prev.right != root) {
            prev = prev.right;
        }
        
        if (prev.right == null) {
            prev.right = root;
            root = root.left;
        } else {
            prev.right = null;
            this.update.accept(root.val, params, res);
            root = root.right;
        }
    }

    return res.stream().mapToInt(Integer::intValue).toArray();
}