104, 二叉树的最大深度

一、题目描述

给定一个二叉树root，返回其最大深度。

二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1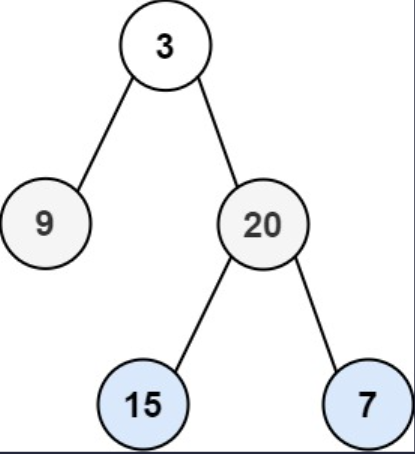

输入: root = [3, 9, 20, null, null, 15, 7]
输出: 3

示例 2
输入: root = [1, null, 2]
输出: 2

提示

• 树中节点的数量在[0, 10⁴]区间内。
• -100 <= Node.val <= 100

相关主题

• 树
• 深度优先搜索
• 广度优先搜索
• 二叉树

二、题解

#[derive(Debug, PartialEq, Eq)]
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Rc<RefCell<TreeNode>>>,
    pub right: Option<Rc<RefCell<TreeNode>>>,
}

impl TreeNode {
    #[inline]
    pub fn new(val: i32) -> Self {
        TreeNode {
            val,
            left: None,
            right: None,
        }
    }
}

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

方法 1: 深度优先搜索

pub fn max_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    const HELPER: fn(Option<Rc<RefCell<TreeNode>>>) -> i32 = |root| {
        if let Some(curr) = root {
            std::cmp::max(
                HELPER(curr.borrow().left.clone()),
                HELPER(curr.borrow().right.clone()),
            ) + 1
        } else {
            0
        }
    };

    HELPER(root)
}

Function<TreeNode, Integer> helper = root -> {
    if (root == null) {
        return 0;
    }
    return Math.max(this.helper.apply(root.left), this.helper.apply(root.right)) + 1;
};

public int maxDepth(TreeNode root) {
    return this.helper.apply(root);
}

方法 2: 广度优先搜索

pub fn max_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    //Self::bfs_iter_1(root)
    Self::bfs_iter_2(root)
}

fn bfs_iter_1(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    let mut max_depth = 0;

    if let Some(root) = root {
        let mut queue = VecDeque::from([(root, 1)]);

        while let Some((curr, level)) = queue.pop_front() {
            max_depth = level;

            if let Some(left) = curr.borrow_mut().left.take() {
                queue.push_back((left, level + 1));
            }
            if let Some(right) = curr.borrow_mut().right.take() {
                queue.push_back((right, level + 1));
            }
        }
    }

    max_depth
}

fn bfs_iter_2(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    let mut max_depth = 0;

    if let Some(root) = root {
        let mut queue = VecDeque::from([root]);

        while !queue.is_empty() {
            let level_len = queue.len();

            for _ in 0..level_len {
                if let Some(curr) = queue.pop_front() {
                    if let Some(left) = curr.borrow_mut().left.take() {
                        queue.push_back(left);
                    }
                    if let Some(right) = curr.borrow_mut().right.take() {
                        queue.push_back(right);
                    }
                }
            }

            max_depth += 1;
        }
    }

    max_depth
}

public int maxDepth(TreeNode root) {
    //return this.bfsIter1(root);
    return this.bfsIter2(root);
}

int bfsIter1(TreeNode root) {
    int maxDepth = 0;

    if (root != null) {
        Deque<Object[]> queue = new ArrayDeque<>() {{
            this.addLast(new Object[]{root, 1});
        }};

        while (!queue.isEmpty()) {
            Object[] obj = queue.removeFirst();
            TreeNode curr = (TreeNode) obj[0];
            int level = (int) obj[1];
            maxDepth = level;

            if (curr.left != null) {
                queue.addLast(new Object[]{curr.left, level + 1});
            }
            if (curr.right != null) {
                queue.addLast(new Object[]{curr.right, level + 1});
            }
        }
    }

    return maxDepth;
}

int bfsIter2(TreeNode root) {
    int maxDepth = 0;

    if (root != null) {
        Deque<TreeNode> queue = new ArrayDeque<>() {{
            this.addLast(root);
        }};

        while (!queue.isEmpty()) {
            int levelSize = queue.size();

            while (levelSize-- > 0) {
                TreeNode curr = queue.removeFirst();

                if (curr.left != null) {
                    queue.addLast(curr.left);
                }
                if (curr.right != null) {
                    queue.addLast(curr.right);
                }
            }

            maxDepth++;
        }
    }

    return maxDepth;
}