2023/12/23大约 3 分钟
一、题目描述
给你一棵完全二叉树的根节点root,求出该树的节点个数。
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第h层,则该层包含1~ 2ʰ个节点。
示例 1
输入: root = [1, 2, 3, 4, 5, 6]
输出: 6
示例 2
输入: root = []
输出: 0
示例 3
输入: root = [1]
输出: 1
提示
- 树中节点的数目范围是
[0, 5 * 10⁴] 0 <= Node.val <= 5 * 10⁴- 题目数据保证输入的树是完全二叉树
进阶
遍历树来统计节点是一种时间复杂度为O(n)的简单解决方案。你可以设计一个更快的算法吗?
相关主题
- 位运算
- 树
- 二分查找
- 二叉树
二、题解
Rust节点定义
#[derive(Debug, PartialEq, Eq)]
pub struct TreeNode {
pub val: i32,
pub left: Option<Rc<RefCell<TreeNode>>>,
pub right: Option<Rc<RefCell<TreeNode>>>,
}
impl TreeNode {
#[inline]
pub fn new(val: i32) -> Self {
TreeNode {
val,
left: None,
right: None,
}
}
}Java节点定义
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}方法 1: 暴力解法
Rust
pub fn count_nodes(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
//Self::dfs_recur(root)
Self::bfs_iter(root)
}
///
/// Time Complexity: O(n)
/// Space Complexity: O(log(n))
///
fn dfs_recur(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
const COUNT: fn(Option<Rc<RefCell<TreeNode>>>) -> i32 = |root| {
if let Some(root) = root {
COUNT(root.borrow().left.clone()) + COUNT(root.borrow().right.clone()) + 1
} else {
0
}
};
COUNT(root)
}
///
/// Time Complexity: O(n)
/// Space Complexity: O(n)
///
fn bfs_iter(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut count = 0;
if let Some(root) = root {
let mut queue = VecDeque::from([root]);
while let Some(curr) = queue.pop_front() {
count += 1;
if let Some(left) = curr.borrow_mut().left.take() {
queue.push_back(left);
}
if let Some(right) = curr.borrow_mut().right.take() {
queue.push_back(right)
}
}
}
count
}Java
public int countNodes(TreeNode root) {
//return this.dfsRecur(root);
return this.bfsIter(root);
}
Function<TreeNode, Integer> count = root -> {
if (root == null) {
return 0;
}
return this.count.apply(root.left) + this.count.apply(root.right) + 1;
};
/**
* Time Complexity: O(n)
* Space Complexity: O(log(n))
*/
int dfsRecur(TreeNode root) {
return this.count.apply(root);
}
/**
* Time Complexity: O(n)
* Space Complexity: O(n)
*/
int bfsIter(TreeNode root) {
int count = 0;
if (root != null) {
Deque<TreeNode> queue = new ArrayDeque<>() {{
this.addLast(root);
}};
while (!queue.isEmpty()) {
TreeNode curr = queue.removeFirst();
count++;
if (curr.left != null) {
queue.addLast(curr.left);
}
if (curr.right != null) {
queue.addLast(curr.right);
}
}
}
return count;
}方法 2: 二叉搜索
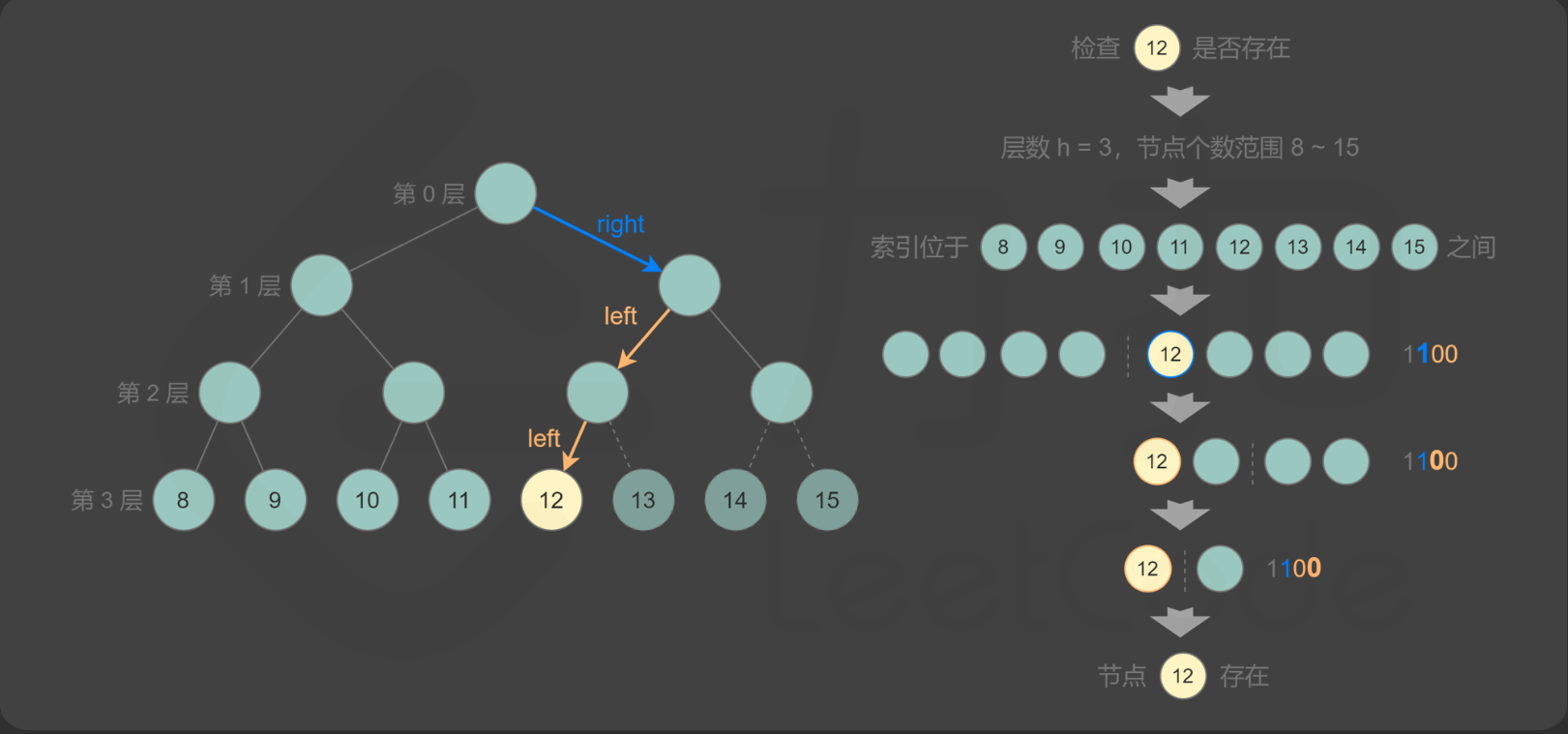
Rust
pub fn count_nodes(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
Self::binary_search(root)
}
///
/// Time Complexity: O(log(n) * log(n))
/// Space Complexity: O(1)
///
fn binary_search(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
if root.is_none() {
return 0;
}
let calc_level: fn(root: Option<Rc<RefCell<TreeNode>>>) -> u32 = |mut root| {
let mut level = 0_u32;
while let Some(curr) = root {
root = curr.borrow().left.clone();
level += 1;
}
level
};
let level = calc_level(root.clone());
let mut min_count = 2_i32.pow(level - 1);
let mut max_count = 2_i32.pow(level);
let exist: fn(Option<Rc<RefCell<TreeNode>>>, i32) -> bool = |mut root, expected_count| {
for c in format!("{:b}", expected_count).chars().skip(1) {
if let Some(curr) = root {
if c == '1' {
root = curr.borrow().right.clone();
} else {
root = curr.borrow().left.clone();
}
if root.is_none() {
return false;
}
}
}
true
};
while min_count < max_count {
let mid = (min_count + max_count) / 2;
if exist(root.clone(), mid) {
min_count = mid + 1;
} else {
max_count = mid;
}
}
min_count - 1
}Java
public int countNodes(TreeNode root) {
return this.binarySearch(root);
}
/**
* Time Complexity: O(log(n) * log(n))
* Space Complexity: O(1)
*/
int binarySearch(TreeNode root) {
if (root == null) {
return 0;
}
Integer level = this.calcLevel.apply(root);
int minCount = (int) Math.pow(2, level - 1);
int maxCount = (int) Math.pow(2, level);
while (minCount < maxCount) {
int mid = (minCount + maxCount) / 2;
if (this.exist.test(root, mid)) {
minCount = mid + 1;
} else {
maxCount = mid;
}
}
return minCount - 1;
}
Function<TreeNode, Integer> calcLevel = root -> {
int level = 0;
TreeNode curr = root;
while (curr != null) {
level++;
curr = curr.left;
}
return level;
};
BiPredicate<TreeNode, Integer> exist = (root, expectedCount) -> {
String path = Integer.toBinaryString(expectedCount);
TreeNode curr = root;
for (int i = 1, size = path.length(); i < size; i++) {
if (path.charAt(i) == '1') {
curr = curr.right;
} else {
curr = curr.left;
}
if (curr == null) {
return false;
}
}
return true;
};