跳至主要內容

572, 另一棵树的子树

Mike大约 4 分钟binary treeeasybinary treedepth first searchstring matchinghash function

一、题目描述

给你两棵二叉树root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在则返回true；否则返回false。

二叉树tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。

示例 1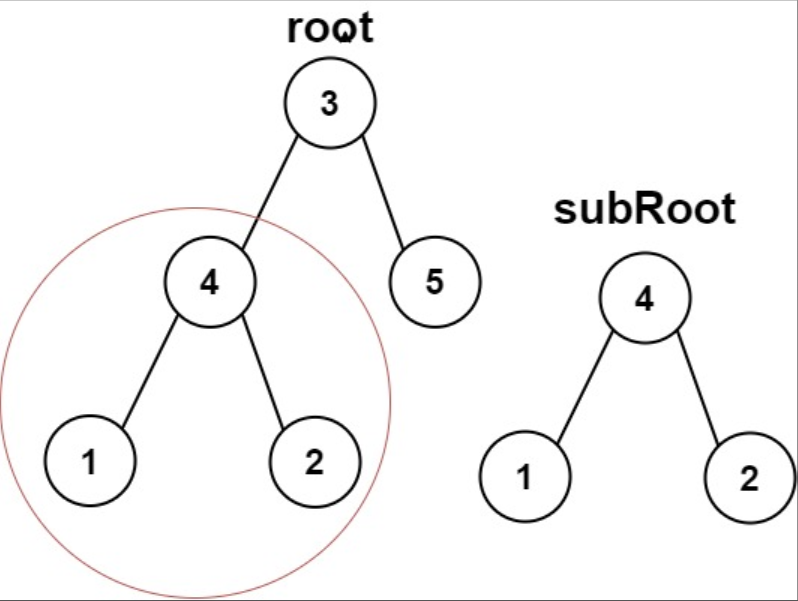

输入: root = [3, 4, 5, 1, 2], subRoot = [4, 1, 2]
输出: true

示例 2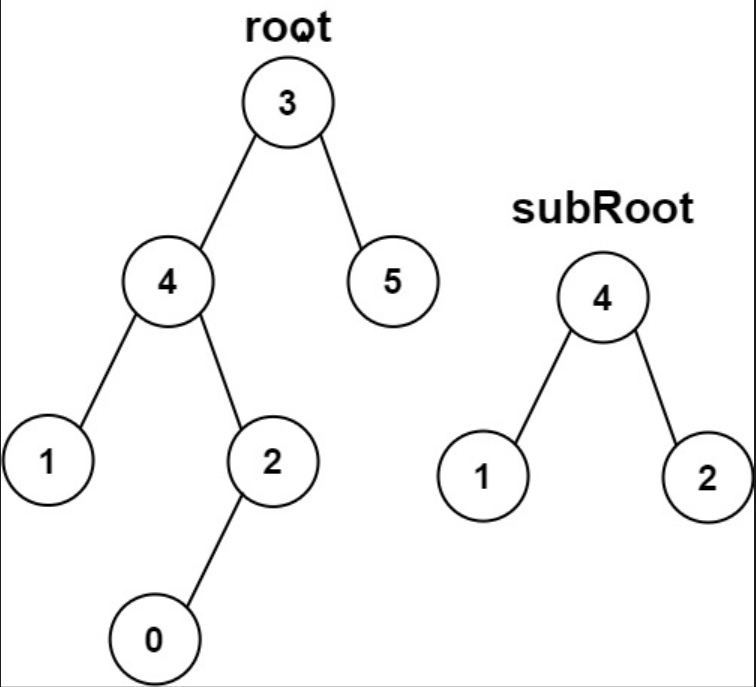

输入: root = [3, 4, 5, 1, 2, null, null, null, null, 0], subRoot = [4, 1, 2]
输出: false

提示

  • root树上的节点数量范围是[1, 2000]
  • subRoot树上的节点数量范围是[1, 1000]
  • -10⁴ <= root.val <= 10⁴
  • -10⁴ <= subRoot.val <= 10⁴

相关主题

  • 树
  • 深度优先搜索
  • 二叉树
  • 字符串匹配
  • 哈希函数

二、题解

#[derive(Debug, PartialEq, Eq)]
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Rc<RefCell<TreeNode>>>,
    pub right: Option<Rc<RefCell<TreeNode>>>,
}

impl TreeNode {
    #[inline]
    pub fn new(val: i32) -> Self {
        TreeNode {
            val,
            left: None,
            right: None,
        }
    }
}

方法 1: 深度优先搜索暴力匹配

pub fn is_subtree(root: Option<Rc<RefCell<TreeNode>>>, sub_root: Option<Rc<RefCell<TreeNode>>>) -> bool {
    Self::dfs_recur_match(root, sub_root)
}

///
/// 时间复杂度: O(|r| * |s|)
/// 空间复杂度: O(max(dr, ds))
///
fn dfs_recur_match(
    root: Option<Rc<RefCell<TreeNode>>>,
    sub_root: Option<Rc<RefCell<TreeNode>>>,
) -> bool {
    const CHECK: fn(Option<Rc<RefCell<TreeNode>>>, Option<Rc<RefCell<TreeNode>>>) -> bool =
        |root, sub_root| match (root, sub_root) {
            (None, None) => true,
            (Some(root), Some(sub_root)) => {
                if root.borrow().val != sub_root.borrow().val {
                    return false;
                }

                CHECK(root.borrow().left.clone(), sub_root.borrow().left.clone())
                    && CHECK(root.borrow().right.clone(), sub_root.borrow().right.clone())
            }
            _ => false,
        };

    const DFS: fn(Option<Rc<RefCell<TreeNode>>>, Option<Rc<RefCell<TreeNode>>>) -> bool =
        |root, sub_root| match root {
            None => false,
            Some(root) => {
                let left = root.borrow().left.clone();
                let right = root.borrow().right.clone();

                CHECK(Some(root), sub_root.clone())
                    || DFS(left, sub_root.clone())
                    || DFS(right, sub_root)
            }
        };

    DFS(root, sub_root)
}

方法 2: 深度优先搜索序列上做串匹配

pub fn is_subtree(root: Option<Rc<RefCell<TreeNode>>>, sub_root: Option<Rc<RefCell<TreeNode>>>) -> bool {
    Self::dfs_sequence_match(root, sub_root)
}

///
/// 时间复杂度: O(|r| + |s|)
/// 空间复杂度: O(|r| + |s|)
///
fn dfs_sequence_match(
    root: Option<Rc<RefCell<TreeNode>>>,
    sub_root: Option<Rc<RefCell<TreeNode>>>,
) -> bool {
    const GET_MAX_ELEMENT: fn(&Option<Rc<RefCell<TreeNode>>>) -> i32 = |root| match root {
        None => i32::MIN,
        Some(curr) => {
            let max_child = std::cmp::max(
                GET_MAX_ELEMENT(&curr.borrow().left),
                GET_MAX_ELEMENT(&curr.borrow().right),
            );

            std::cmp::max(max_child, curr.borrow().val)
        }
    };

    let max_elem = std::cmp::max(GET_MAX_ELEMENT(&root), GET_MAX_ELEMENT(&sub_root));
    let (l_null, r_null) = (max_elem + 1, max_elem + 2);

    let get_dfs_order = |root| {
        let mut vals = vec![];

        const GET_DFS_ORDER: fn(Option<Rc<RefCell<TreeNode>>>, &mut Vec<i32>, i32, i32) =
            |root, vals, l_null, r_null| {
                if let Some(curr) = root {
                    vals.push(curr.borrow().val);
                    let left = curr.borrow_mut().left.take();
                    let right = curr.borrow_mut().right.take();

                    if left.is_some() {
                        GET_DFS_ORDER(left, vals, l_null, r_null);
                    } else {
                        vals.push(l_null);
                    }

                    if right.is_some() {
                        GET_DFS_ORDER(right, vals, l_null, r_null);
                    } else {
                        vals.push(r_null);
                    }
                }
            };

        GET_DFS_ORDER(root, &mut vals, l_null, r_null);

        vals
    };
    let root_vals = get_dfs_order(root);
    let sub_vals = get_dfs_order(sub_root);

    let kmp = || {
        let root_len = root_vals.len();
        let sub_len = sub_vals.len();
        let mut fail = vec![-1; sub_len];
        let mut j = -1_i32;

        for i in 1..sub_len {
            while j != -1 && sub_vals[i] != sub_vals[(j + 1) as usize] {
                j = fail[j as usize]
            }
            if sub_vals[i] == sub_vals[(j + 1) as usize] {
                j += 1;
            }
            fail[i] = j;
        }

        j = -1;
        for i in 0..root_len {
            while j != -1 && root_vals[i] != sub_vals[(j + 1) as usize] {
                j = fail[j as usize];
            }
            if root_vals[i] == sub_vals[(j + 1) as usize] {
                j += 1;
            }
            if (j + 1) as usize == sub_len {
                return true;
            }
        }

        false
    };

    kmp()
}