538, 把二叉搜索树转换为累加树

Mike大约 3 分钟

一、题目描述

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点node的新值等于原树中大于或等于node.val的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

注意：本题和1038: 从二叉搜索树到更大和树open in new window相同

示例 1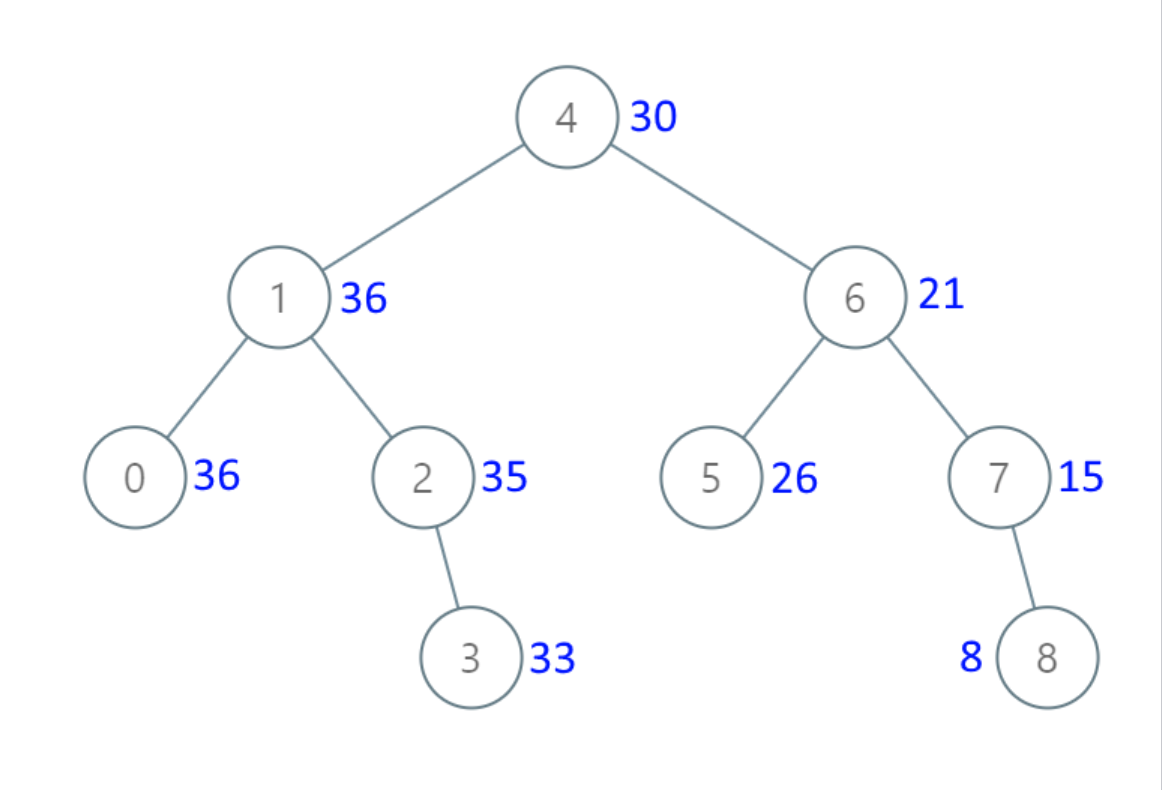

输入: root = [4, 1, 6, 0, 2, 5, 7, null, null, null, 3, null, null, null, 8]
输出: [30, 36, 21, 36, 35, 26, 15, null, null, null, 33, null, null, null, 8]

示例 2
输入: root = [0, null, 1]
输出: [1, null, 1]

示例 3
输入: root = [1, 0, 2]
输出: [3, 3, 2]

示例 4
输入: root = [3, 2, 4, 1]
输出: [7, 9, 4, 10]

提示

树中的节点数介于0和10⁴之间。
每个节点的值介于-10⁴和10⁴之间。
树中的所有值互不相同。
给定的树为二叉搜索树。

相关主题

树
深度优先搜索
二叉搜索树
二叉树

二、题解

#[derive(Debug, PartialEq, Eq)]
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Rc<RefCell<TreeNode>>>,
    pub right: Option<Rc<RefCell<TreeNode>>>,
}

impl TreeNode {
    #[inline]
    pub fn new(val: i32) -> Self {
        TreeNode {
            val,
            left: None,
            right: None,
        }
    }
}

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

方法 1: 镜像中序遍历

pub fn convert_bst(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
    //Self::mirror_in_order_recur_1(root)
    //Self::mirror_in_order_iter_1(root)
    Self::mirror_in_order_recur_2(root)
}

fn mirror_in_order_recur_1(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
    let mut sum = 0;
    const TRAVERSAL: fn(Option<Rc<RefCell<TreeNode>>>, &mut i32) = |root, sum| {
        if let Some(curr) = root {
            TRAVERSAL(curr.borrow().right.clone(), sum);

            curr.borrow_mut().val += *sum;
            *sum = curr.borrow().val;

            TRAVERSAL(curr.borrow().left.clone(), sum);
        }
    };

    TRAVERSAL(root.clone(), &mut sum);

    root
}

fn mirror_in_order_iter_1(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
    if let Some(root) = root.clone() {
        let mut sum = 0;
        let mut stack = vec![Ok(root)];

        while let Some(curr) = stack.pop() {
            match curr {
                Ok(node) => {
                    if let Some(left) = node.borrow().left.clone() {
                        stack.push(Ok(left));
                    }

                    stack.push(Err(node.clone()));

                    if let Some(right) = node.borrow().right.clone() {
                        stack.push(Ok(right));
                    }
                }
                Err(target) => {
                    target.borrow_mut().val += sum;
                    sum = target.borrow().val;
                }
            }
        }
    }

    root
}

fn mirror_in_order_recur_2(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
    const TRAVERSAL: fn(Option<Rc<RefCell<TreeNode>>>, i32) -> i32 = |root, sum| match root {
        None => sum,
        Some(curr) => {
            let r_sum = TRAVERSAL(curr.borrow().right.clone(), sum);

            curr.borrow_mut().val += r_sum;

            TRAVERSAL(curr.borrow().left.clone(), curr.borrow().val)
        }
    };

    TRAVERSAL(root.clone(), 0);

    root
}

public TreeNode convertBST(TreeNode root) {
    //return mirrorInorderRecur1(root);
    //return mirrorInorderIter1(root);
    return mirrorInorderRecur2(root);
}

BiConsumer<TreeNode, int[]> traversal1 = (root, sum) -> {
    if (root == null) {
        return;
    }
    this.traversal1.accept(root.right, sum);

    root.val += sum[0];
    sum[0] = root.val;

    this.traversal1.accept(root.left, sum);
};

TreeNode mirrorInorderRecur1(TreeNode root) {
    int[] sum = new int[]{0};
    this.traversal1.accept(root, sum);
    return root;
}

TreeNode mirrorInorderIter1(TreeNode root) {
    if (root != null) {
        int sum = 0;
        Deque<Object[]> stack = new ArrayDeque<>() {{
            this.push(new Object[]{false, root});
        }};

        while (!stack.isEmpty()) {
            Object[] objs = stack.pop();
            boolean isTarget = (boolean) objs[0];
            TreeNode curr = (TreeNode) objs[1];

            if (isTarget) {
                curr.val += sum;
                sum = curr.val;
            } else {
                if (curr.left != null) {
                    stack.push(new Object[]{false, curr.left});
                }

                stack.push(new Object[]{true, curr});

                if (curr.right != null) {
                    stack.push(new Object[]{false, curr.right});
                }
            }
        }
    }

    return root;
}

BiFunction<TreeNode, Integer, Integer> traversal2 = (root, sum) -> {
    if (root == null) {
        return sum;
    }
    Integer r_sum = this.traversal2.apply(root.right, sum);

    root.val += r_sum;

    return this.traversal2.apply(root.left, root.val);
};

TreeNode mirrorInorderRecur2(TreeNode root) {
    this.traversal2.apply(root, 0);

    return root;
}

方法 2: Morris镜像中序遍历

pub fn convert_bst(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
    let mut root_node = root.clone();
    let mut sum = 0;

    while let Some(curr) = root_node {
        let right = curr.borrow().right.clone();

        if right.is_some() {
            let mut prev_node = right.clone();

            while let Some(ref prev) = prev_node {
                let left = prev.borrow().left.clone();
                if left.is_none() || left == Some(curr.clone()) {
                    break;
                } else {
                    prev_node = left;
                }
            }

            match prev_node {
                None => break, // this is a mark code
                Some(prev) => {
                    let mut prev = prev.borrow_mut();

                    if let Some(_) = prev.left.take() {
                        curr.borrow_mut().val += sum;
                        sum = curr.borrow().val;
                        root_node = curr.borrow().left.clone();
                    } else {
                        prev.left = Some(curr.clone());
                        root_node = right;
                    }
                }
            }
        } else {
            curr.borrow_mut().val += sum;
            sum = curr.borrow().val;
            root_node = curr.borrow().left.clone();
        };
    }

    root
}

public TreeNode convertBST(TreeNode root) {
    TreeNode curr = root;
    int sum = 0;

    while (curr != null) {
        if (curr.right != null) {
            TreeNode prev = curr.right;

            while (prev.left != null && prev.left != curr) {
                prev = prev.left;
            }
            
            if (prev.left == null) {
                prev.left = curr;
                curr = curr.right;
            } else {
                prev.left = null;
                curr.val += sum;
                sum = curr.val;
                curr = curr.left;
            }
        } else {
            curr.val += sum;
            sum = curr.val;
            curr = curr.left;
        }
    }

    return root;
}

538, 把二叉搜索树转换为累加树

# 一、题目描述

# 二、题解

# 方法 1: 镜像中序遍历

# 方法 2: Morris镜像中序遍历

一、题目描述

二、题解

方法 1: 镜像中序遍历

方法 2: Morris镜像中序遍历