404, Sum of Left Leaves

I Problem

Given the root of a binary tree, return the sum of all left leaves.

A leaf is a node with no children. A left leaf is a leaf that is the left child of another node.

Example 1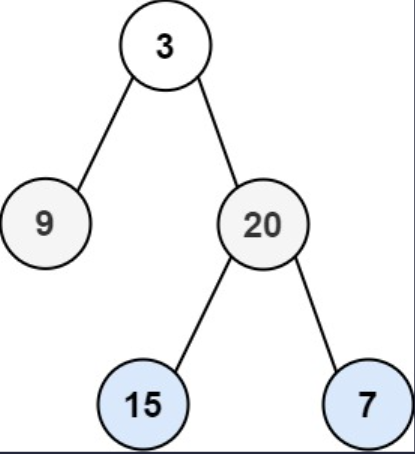

Input: root = [3, 9, 20, null, null, 15, 7]
Output: 24
Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.

Example 2
Input: root = [1]
Output: 0

Constraints

• The number of nodes in the tree is in the range [1, 1000].
• -1000 <= Node.val <= 1000

Related Topics

• Tree
• Depth-First Search
• Breadth-First Search
• Binary Tree

II Solution

#[derive(Debug, PartialEq, Eq)]
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Rc<RefCell<TreeNode>>>,
    pub right: Option<Rc<RefCell<TreeNode>>>,
}

impl TreeNode {
    #[inline]
    pub fn new(val: i32) -> Self {
        TreeNode {
            val,
            left: None,
            right: None,
        }
    }
}

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

Approach 1: Depth-First Search

pub fn sum_of_left_leaves(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    //Self::dfs_recur_1(root)
    //Self::dfs_recur_2(root)
    Self::dfs_iter(root)
}

fn dfs_recur_1(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    let mut sum = 0;
    const RECUR: fn(Option<Rc<RefCell<TreeNode>>>, bool, &mut i32) = |root, is_left, sum| {
        if let Some(curr) = root {
            let left = curr.borrow_mut().left.take();
            let right = curr.borrow_mut().right.take();
            match (left, right) {
                (None, None) => {
                    if is_left {
                        *sum += curr.borrow().val;
                    }
                }
                (left, right) => {
                    if left.is_some() {
                        RECUR(left, true, sum);
                    }
                    if right.is_some() {
                        RECUR(right, false, sum);
                    }
                }
            }
        }
    };

    RECUR(root, false, &mut sum);

    sum
}

fn dfs_recur_2(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    const RECUR: fn(Option<Rc<RefCell<TreeNode>>>, bool) -> i32 = |root, is_left| match root {
        None => 0,
        Some(curr) => {
            let left = curr.borrow_mut().left.take();
            let right = curr.borrow_mut().right.take();
            match (left, right) {
                (None, None) => {
                    if is_left {
                        curr.borrow().val
                    } else {
                        0
                    }
                }
                (left, right) => RECUR(left, true) + RECUR(right, false),
            }
        }
    };

    RECUR(root, false)
}

fn dfs_iter(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    let mut sum = 0;

    if let Some(root) = root {
        let mut stack = vec![(root, false)];

        while let Some((curr, is_left)) = stack.pop() {
            let left = curr.borrow_mut().left.take();
            let right = curr.borrow_mut().right.take();

            if left.is_none() && right.is_none() && is_left {
                sum += curr.borrow().val;
            }
            if let Some(right) = right {
                stack.push((right, false));
            }
            if let Some(left) = left {
                stack.push((left, true));
            }
        }
    }

    sum
}

public int sumOfLeftLeaves(TreeNode root) {
    //return this.dfsRecur1(root);
    //return this.dfsRecur2(root);
    return this.dfsIter(root);
}

@FunctionalInterface
interface TriConsumer<A, B, C> {
    void accept(A a, B b, C c);
}
TriConsumer<TreeNode, Boolean, int[]> recur1 = (root, isLeft, sum) -> {
    if (root == null) {
        return;
    }
    if (root.left == null && root.right == null) {
        if (isLeft) {
            sum[0] += root.val;
        }
    } else {
        if (root.left != null) {
            this.recur1.accept(root.left, true, sum);
        }
        if (root.right != null) {
            this.recur1.accept(root.right, false, sum);
        }
    }
};
int dfsRecur1(TreeNode root) {
    int[] sum = new int[]{0};
    this.recur1.accept(root, false, sum);
    return sum[0];
}

BiFunction<TreeNode, Boolean, Integer> recur2 = (root, isLeft) -> {
    if (root == null) {
        return 0;
    }
    if (root.left == null && root.right == null) {
        if (isLeft) {
            return root.val;
        } else {
            return 0;
        }
    } else {
        return this.recur2.apply(root.left, true) + this.recur2.apply(root.right, false);
    }
};
int dfsRecur2(TreeNode root) {
    return this.recur2.apply(root, false);
}

int dfsIter(TreeNode root) {
    int sum = 0;

    if (root != null) {
        Deque<Object[]> stack = new ArrayDeque<>() {{
            this.push(new Object[]{root, false});
        }};

        while (!stack.isEmpty()) {
            Object[] objs = stack.pop();
            TreeNode curr = (TreeNode) objs[0];
            boolean isLeft = (boolean) objs[1];

            if (curr.left == null && curr.right == null && isLeft) {
                sum += curr.val;
            }
            if (curr.right != null) {
                stack.push(new Object[]{curr.right, false});
            }
            if (curr.left != null) {
                stack.push(new Object[]{curr.left, true});
            }
        }
    }

    return sum;
}

Approach 2: Breadth-First Search

pub fn sum_of_left_leaves(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    Self::bfs_iter(root)
}

fn bfs_iter(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    let mut sum = 0;

    if let Some(root) = root {
        let mut queue = VecDeque::from([(root, false)]);

        while let Some((curr, is_left)) = queue.pop_front() {
            let left = curr.borrow_mut().left.take();
            let right = curr.borrow_mut().right.take();

            if left.is_none() && right.is_none() && is_left {
                sum += curr.borrow().val;
            }
            if let Some(left) = left {
                queue.push_back((left, true));
            }
            if let Some(right) = right {
                queue.push_back((right, false));
            }
        }
    }

    sum
}

public int sumOfLeftLeaves(TreeNode root) {
    return this.bfsIter(root);
}

int bfsIter(TreeNode root) {
    int sum = 0;

    if (root != null) {
        Deque<Object[]> queue = new ArrayDeque<>() {{
            this.addLast(new Object[]{root, false});
        }};

        while (!queue.isEmpty()) {
            Object[] objs = queue.removeFirst();
            TreeNode curr = (TreeNode) objs[0];
            boolean isLeft = (boolean) objs[1];

            if (curr.left == null && curr.right == null && isLeft) {
                sum += curr.val;
            }
            if (curr.left != null) {
                queue.addLast(new Object[]{curr.left, true});
            }
            if (curr.right != null) {
                queue.addLast(new Object[]{curr.right, false});
            }
        }
    }

    return sum;
}